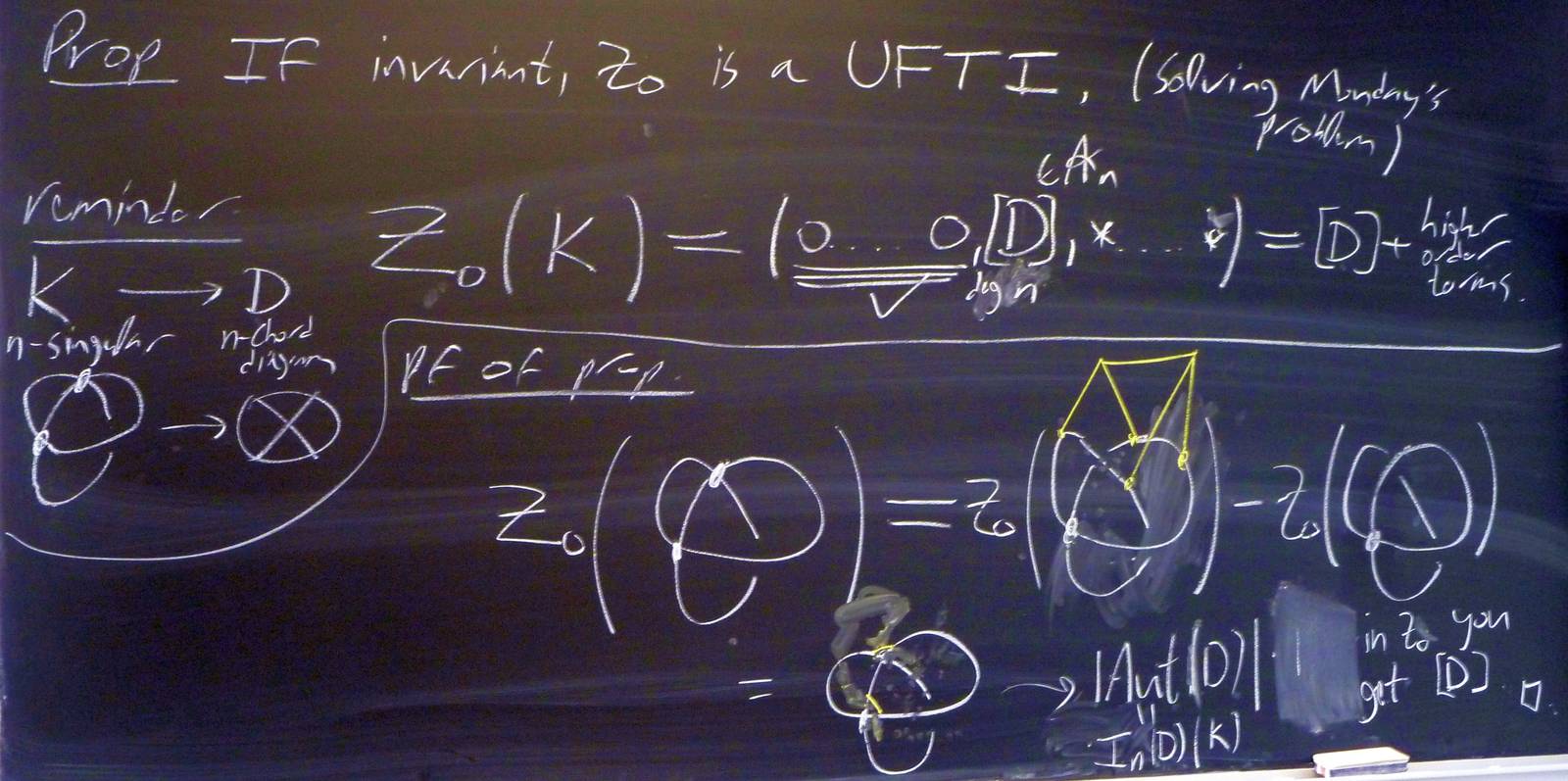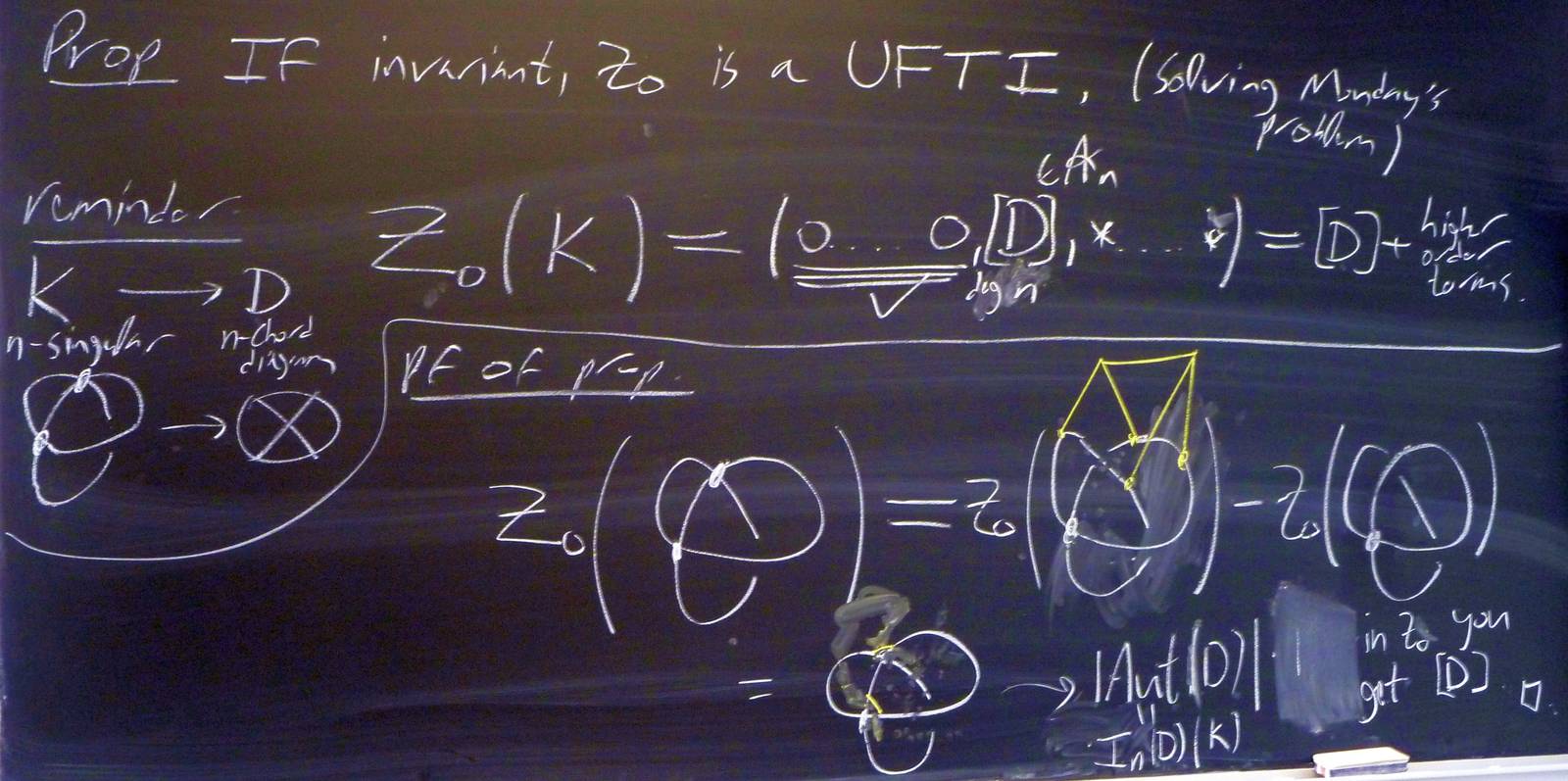
| AKT14-{ | hide text |
| 140407-105125: | The Friday-Wednesday relation. |
| 140407-104608: | The full Chern-Simons path integrals with ghosts, and its perturbative expansion. |
| 140407-102836: | Random formulas. |
| 140407-101549: | Faddeev-Popov. |
| 140404-110419: | Horizontal compositions, generating tangles. |
| 140404-105953: | The case of tangles. |
| 140404-104947: | General algebraic structures. |
| 140404-103527: | $A$-expansions. |
| 140404-102655: | General facts about $gr$. |
| 140404-102635: | Notices and reminders about expansions. |
| 140326-110047: | Pulling back commutes with pushing forward. |
| 140326-105711: | The proof of $dZ_0=A\cdot dZ_0$. |
| 140326-103805: | Understanding and cancelling the anomaly. |
| 140326-102116: | Review of the anomaly 2-form. |
| 140324-113339: | Exercises. |
| 140324-110108: | ${\mathcal A}$ is a bi-algebra (2). |
| 140324-105310: | ${\mathcal A}$ is a bi-algebra. |
| 140324-104340: | Examples of bi-algebras. |
| 140324-103310: | Co-algebras, bi-algebras. |
| 140324-102709: | Reminders, algebras. |
| 140321-110354: | $\det(Q+\epsilon P)$ (2). |
| 140321-105354: | $\det(Q+\epsilon P)$. |
| 140321-104306: | Faddeev-Popov in the case of rotations on ${\mathbb R}^2$. |
| 140321-103733: | The Faddeev-Popov determinant formula. |
| 140319-110415: | The anomaly (3). |
| 140319-105818: | The anomaly (2). |
| 140319-104246: | The anomaly. |
| 140319-103040: | Vanishing of the non-anomalous hidden faces. |
| 140317-105925: | Universal PBW. |
| 140317-104923: | PBW. |
| 140317-103729: | $W_{\mathfrak g}$. |
| 140317-102557: | ${\mathcal U}({\mathfrak g})$. |
| 140314-110347: | Naive expectations for perturbation theory. |
| 140314-110240: | Finally, the Chern-Simon path integral. |
| 140314-103456: | Insolubility of the quintic. |
| 140312-110420: | Cancellation of most hidden faces (2). |
| 140312-105957: | Cancellation of most hidden faces. |
| 140312-104503: | $Z_0$ is a UFTI (if invariant). |
| 140312-103108: | Reminders, a better formula for $Z_0$. |
| 140310-100021: | A preview of bi-algebras. |
| 140310-095320: | $4T$ for $gl(N)$. |
| 140310-094743: | The $so(N)$ case. |
| 140310-094353: | Further $gl(N)$ computations. |
| 140310-093925: | A $gl(N)$ computation. |
| 140310-092839: | The $gl(N)$ structure constants. |
| 140310-091619: | Reminders. |
| 140307-110330: | An iterated integral formula for the holonomy. |
| 140307-105409: | The Chern-Simons form, holonomies. |
| 140307-104129: | Motivation from physics, economics, and mathematics. |
| 140307-101950: | Some formulas for gauge transformations. |
| 140305-111609: | Chern-Simons and curvatures. |
| 140305-110203: | ${\mathcal A}$ arises! |
| 140305-110128: | The adjoint of the graph differential (3). |
| 140305-105737: | The adjoint of the graph differential (2). |
| 140305-105506: | The adjoint of the graph differential. |
| 140305-105317: | $Z_0$. |
| 140305-103551: | Handout support. |
| 140303-110402: | Not all invariant tensors arise this way. |
| 140303-110019: | $W_{{\mathfrak g},R}$ satisfies IHX, AS, STU. |
| 140303-104444: | Well-definededness of $W_{{\mathfrak g},R}$ (2). |
| 140303-103342: | Well-definededness of $W_{{\mathfrak g},R}$. |
| 140303-102902: | Informal `universallity' of the construction. |
| 140303-102801: | The construction of $W_{{\mathfrak g},R}$. |
| 140303-101621: | Reminders: the structure constants. |
| 140228-105841: | Very naive gauge theory (2). |
| 140228-105256: | Very naive gauge theory. |
| 140228-104034: | Some diagrams. |
| 140226-110208: | Graph cohomology and $\Omega_{dR}^\ast(\Gamma)$ (3). |
| 140226-104550: | Graph cohomology and $\Omega_{dR}^\ast(\Gamma)$ (2). |
| 140226-103415: | Graph cohomology and $\Omega_{dR}^\ast(\Gamma)$. |
| 140224-110146: | The structure constants. |
| 140224-105632: | Metrized Lie algebras. |
| 140224-104701: | Constructing weight systems from Lie algebras. |
| 140224-103753: | Lie algebras and representations. |
| 140224-102332: | Reminders. |
| 140214-110030: | Perturbed Gaussian integration and Feynman diagrams (2). |
| 140214-105240: | Perturbed Gaussian integration and Feynman diagrams. |
| 140214-103957: | Inverting the Laplacian. |
| 140214-103102: | $L^-$ and $\Delta$. |
| 140214-102429: | The $\delta$-function as an integral. |
| 140214-101840: | Notes and plans, our section. |
| 140212-110205: | The case of a knot in ${\mathbb R}^3$. |
| 140212-105540: | Dealing with infra-red. |
| 140212-103645: | Review of Fulton-MacPherson and the basic properties. |
| 140210-110136: | ${\mathcal A}(\bigcirc)\simeq{\mathcal A}(\uparrow)$. |
| 140210-105758: | Proof of the invariance principle. |
| 140210-105231: | The invariance principle. |
| 140210-104841: | Proof of bracket-rise (2). |
| 140210-104537: | Proof of bracket-rise. |
| 140210-102624: | A table of dimensions, statement of bracket-rise. |
| 140207-181713: | Homework Assignment 5. |
| 140207-110017: | Gauge fixing and Hodge theory. |
| 140207-105119: | The formula for $d^{-1}$. |
| 140207-104454: | Stokes for pushforwards. |
| 140207-104103: | Reminders on pushforwards. |
| 140205-110540: | Manifolds with corners. |
| 140205-104349: | Implementation. |
| 140205-103009: | Clustering. |
| 140203-111929: | The Fundamental Theorem is equivalent to a UFTI (2). |
| 140203-105428: | The Fundamental Theorem is equivalent to a UFTI. |
| 140203-104540: | The fundamental theorem, universal finite type invariants. |
| 140203-103129: | The 4T relation and $\mathcal A$-spaces. |
| 140203-102113: | Notes and reminders. |
| 140131-183811: | Homework Assignment 4, Questions 1-2-3. |
| 140131-110316: | Pushforwards. |
| 140131-105659: | An integral formula for $d^{-1}$. |
| 140131-104019: | $d^{-1}$ and linking numbers as intersection numbers. |
| 140131-102906: | Reminders, 1-forms, 2-forms, cycles. |
| 140129-110420: | Sign issues. |
| 140129-105603: | A blatantly false theorem. |
| 140129-105306: | The configuration space $C_D({\mathbb R}^3,\gamma)$. |
| 140129-103734: | Swaddling maps and framings. |
| 140129-102632: | Goals, a new formula for $sl_2$. |
| 140127-110314: | The 4T relation. |
| 140127-105732: | The FI relation. |
| 140127-105435: | Weight systems and finiteness. |
| 140127-104216: | $n$-singular knots and $n$-chord diagrams. |
| 140127-103346: | The $n$th derivative is constant. |
| 140127-102321: | HOMFLY-PT and Conway. |
| 140127-101400: | Notes and reminders. |
| 140124-190950: | Homework Assignment 3, Question 3. |
| 140124-190949: | Homework Assignment 3, Questions 1 and 2. |
| 140124-105724: | The second moments (2). |
| 140124-104736: | The second moments. |
| 140124-103755: | Moments of Gaussian integrals. |
| 140124-102426: | Gaussian integration of arbitrary quadratics. |
| 140124-101522: | Notices and today's goal. |
| 140122-110556: | Little on Frenet-Serret. |
| 140122-105652: | Framings and SO(3). |
| 140122-104159: | Framings. |
| 140122-102833: | Reminders. |
| 140120-110110: | Jones is a FT series, proof. |
| 140120-105912: | The Jones skein relation. |
| 140120-103943: | Jones is a FT series. |
| 140120-103110: | The definition of finite-type. |
| 140120-102454: | $n$-singular knots and differentiating invariants. |
| 140120-101022: | Notices and the proper spelling on Wensday. |
| 140120-100933: | Reminder on Kauffman and Jones. |
| 140117-185407: | Just a riddle, not a HW problem. |
| 140117-185406: | Homework Assignment 2, Questions 2-3. |
| 140117-185405: | Homework Assignment 2, Question 1. |
| 140117-110102: | Volumes of spheres. |
| 140117-104951: | The most-basic Gaussian integration. |
| 140117-103851: | Minimization problems. |
| 140117-102828: | The goal for 2-3 Fridays. |
| 140115-110235: | Properties of $sl_1$. |
| 140115-105829: | Swaddling. |
| 140115-104033: | The naive self-linking integral. |
| 140115-102559: | Reminders and degrees. |
| 140113-110000: | The definition of the Jones polynomial. |
| 140113-104126: | Ikke-invariance under R1 and the writhe. |
| 140113-103403: | Invariance under R2 and R3. |
| 140113-103143: | Computation for the trefoil. |
| 140113-103130: | Definition of the Kauffman bracket. |
| 140113-100835: | Notifications. |
| 140110-192042: | Homework 1 (3). |
| 140110-192041: | Homework 1 (2). |
| 140110-191441: | Homework 1. |
| 140110-105842: | Pythagoras' theorem. |
| 140110-104943: | Recovering classical mechanics. |
| 140110-102352: | Trotter's formula. |
| 140110-102238: | Arriving at Schroedinger. |
| 140108-120508: | An ugly explicit formula for the linking number integral. |
| 140108-115840: | Alternative choice of volume forms. |
| 140108-115225: | Invariance of the linking number integral. |
| 140108-115001: | Computing the linking number integral. |
| 140108-113910: | The linking number as an integral. |
| 140108-113457: | Invariance of the linking number sum. |
| 140108-112656: | The linking number as a sum over xings. |
| 140108-111537: | Scheduling. |
| 140106-120556: | Invariance of 3-colourings under Reidemeister moves. |
| 140106-120118: | Reidemeister theorem and 3-colourings. |
| 140106-114501: | Defining knots. |
| } |
Notes for BBS/AKT14-140312-104503.jpg: [edit]