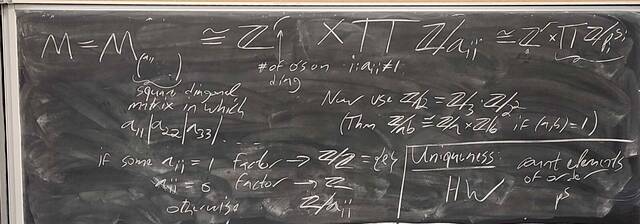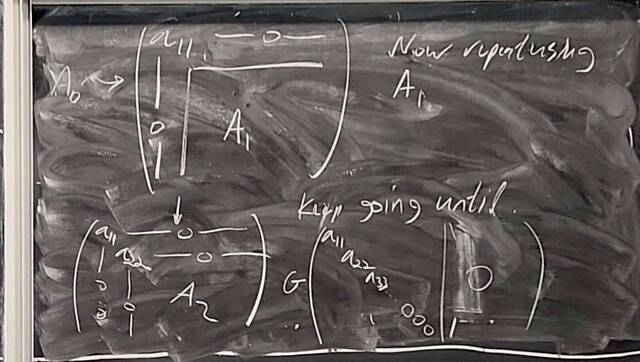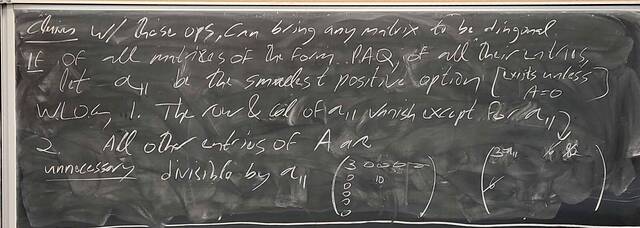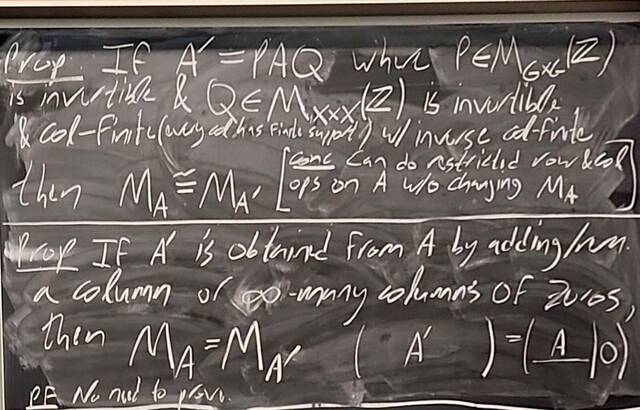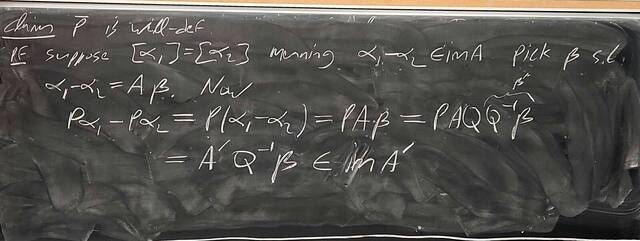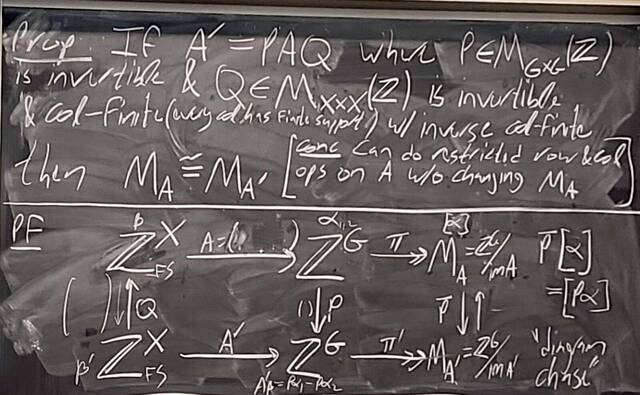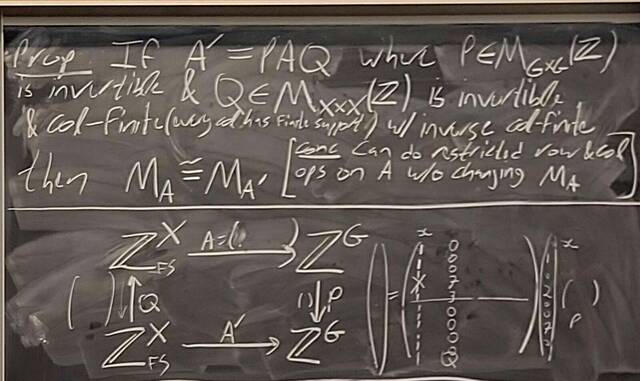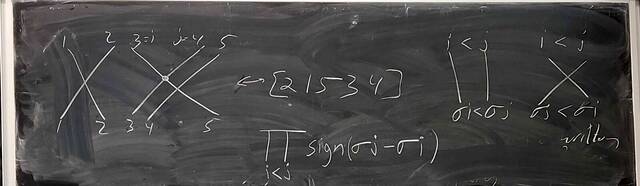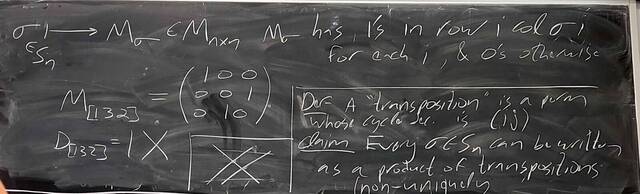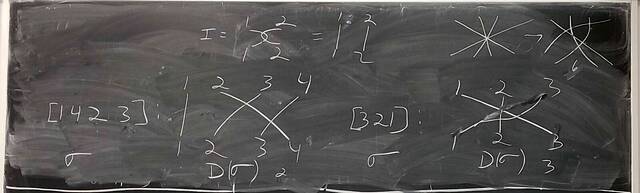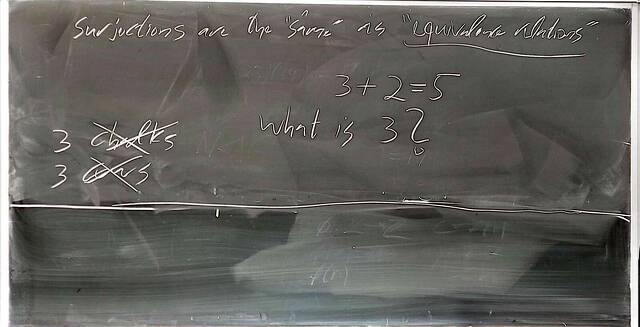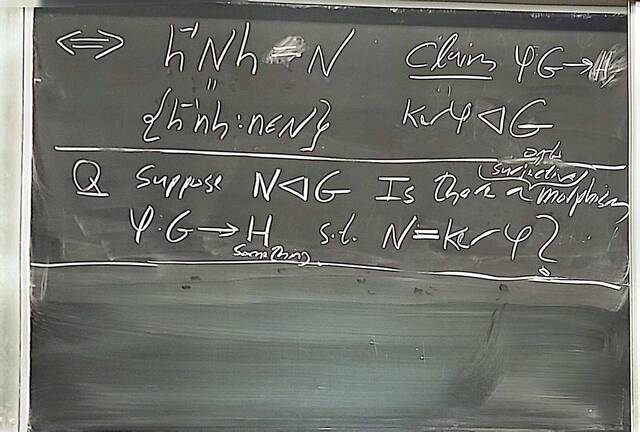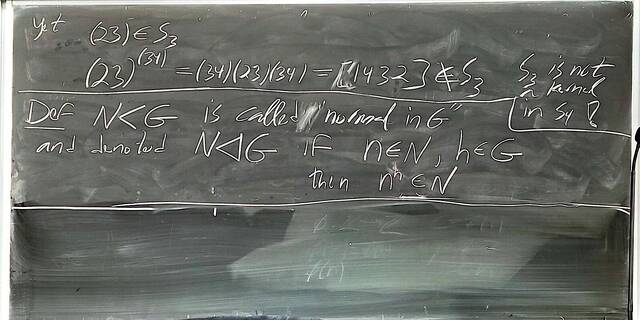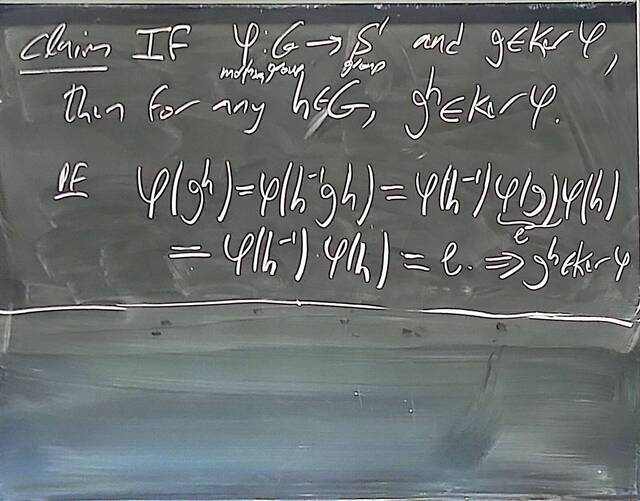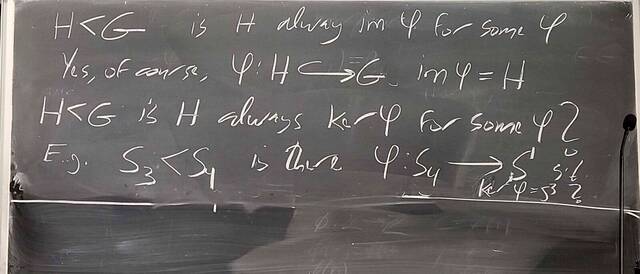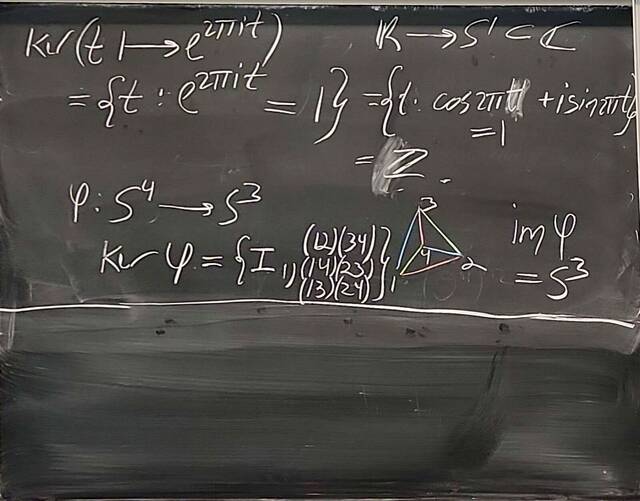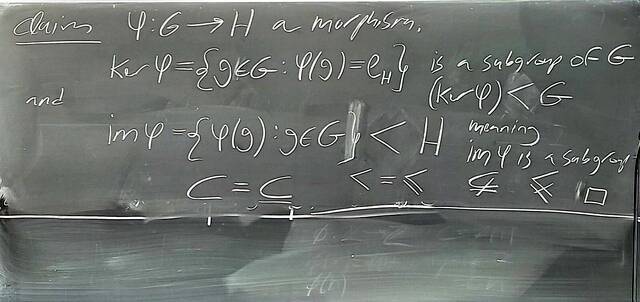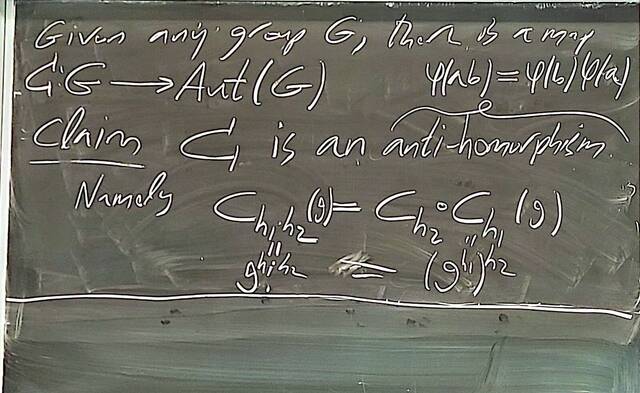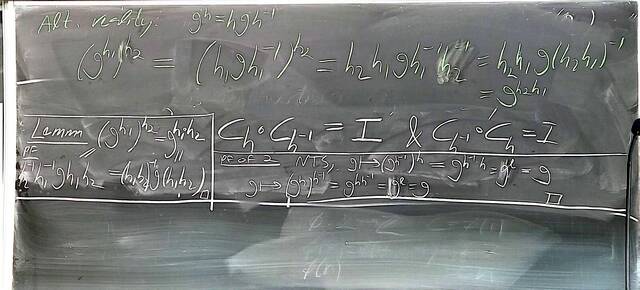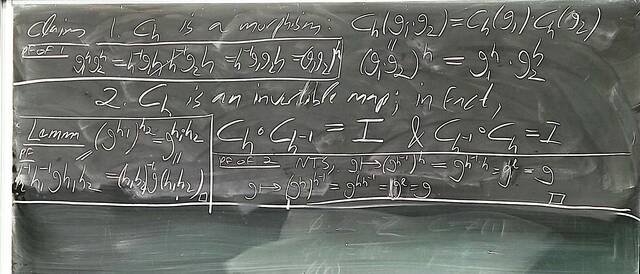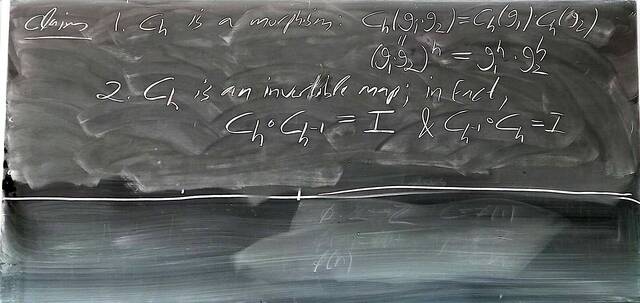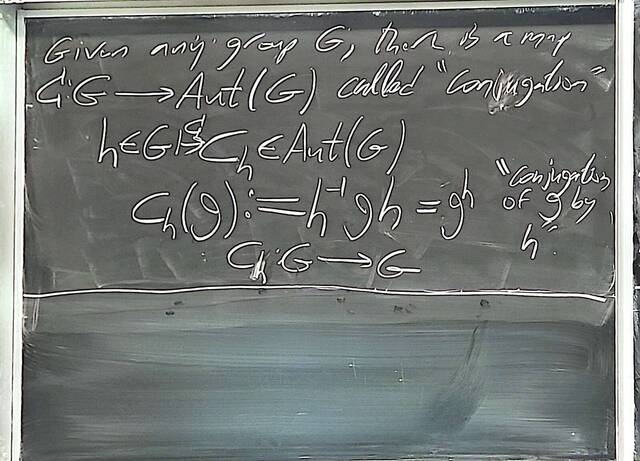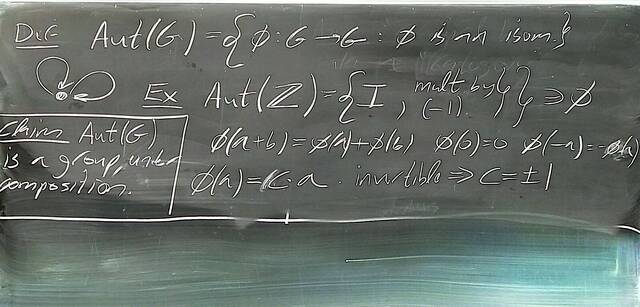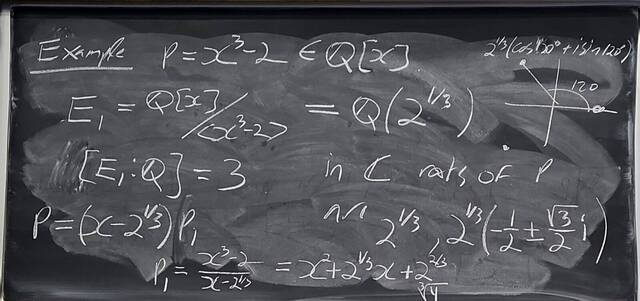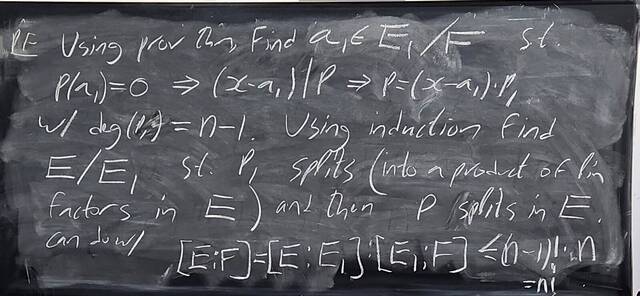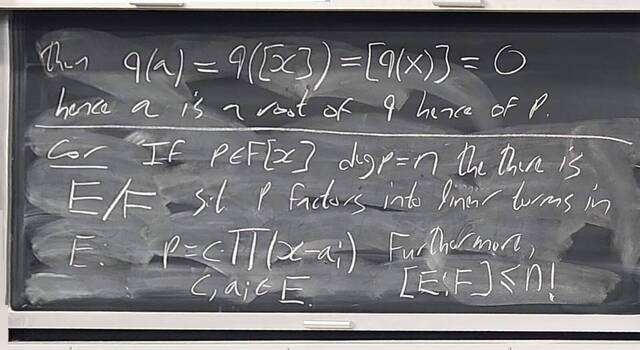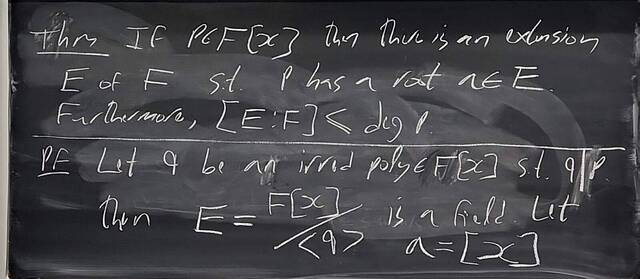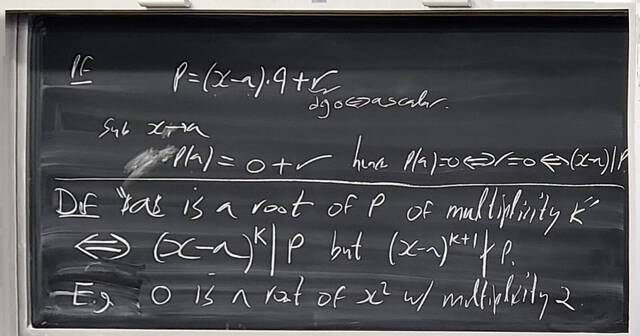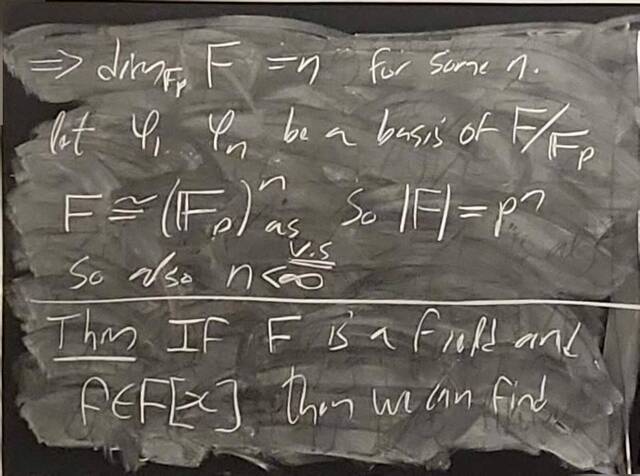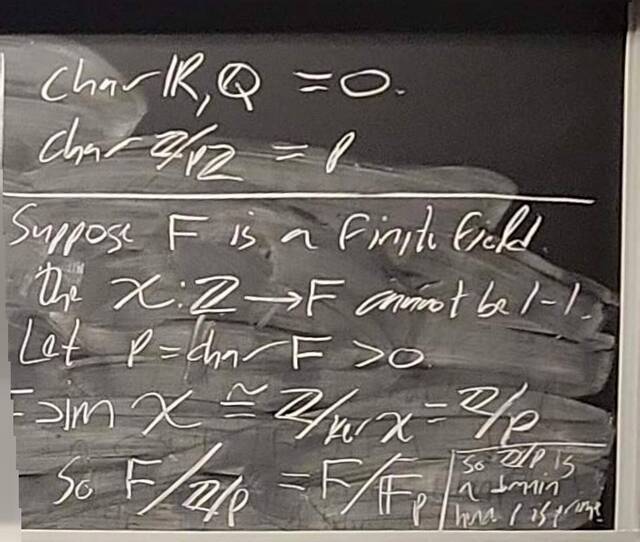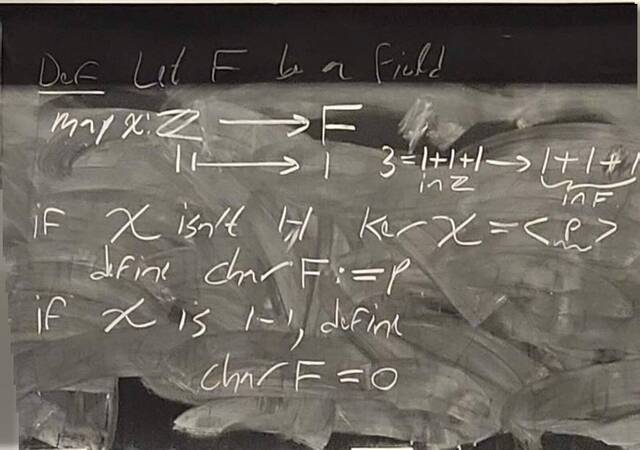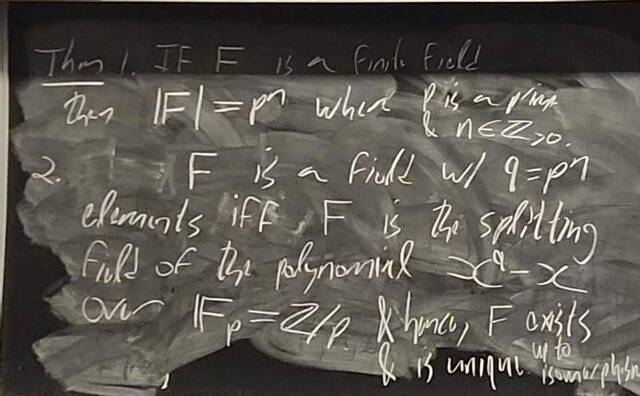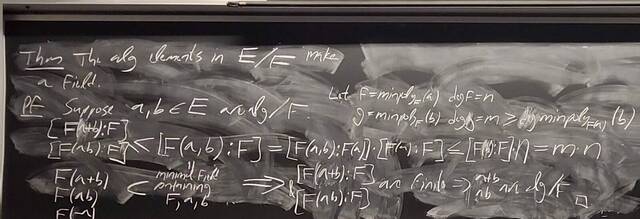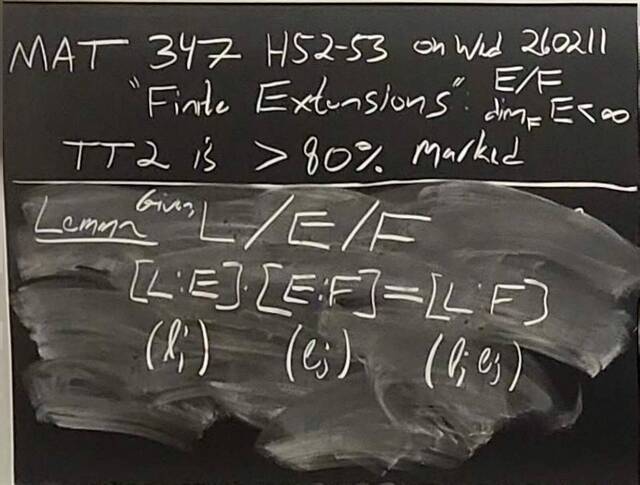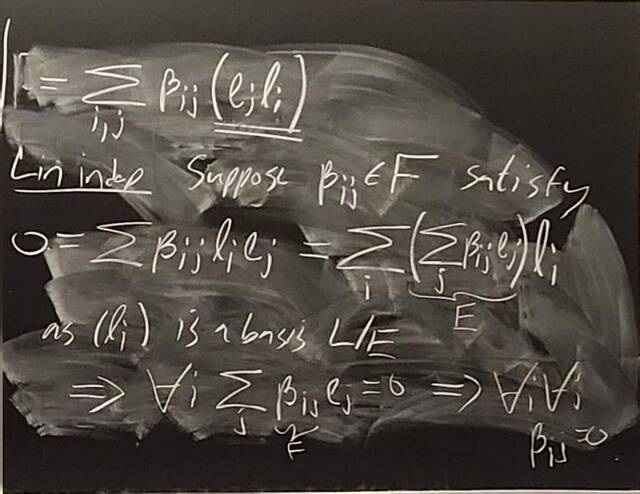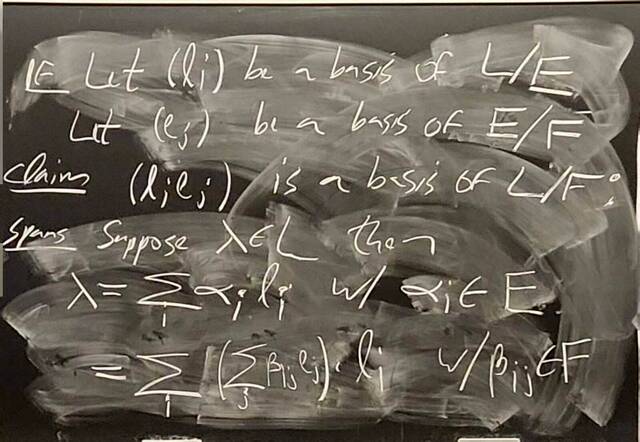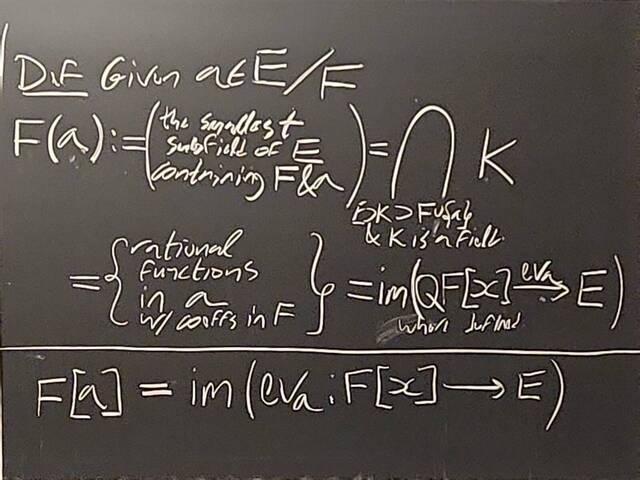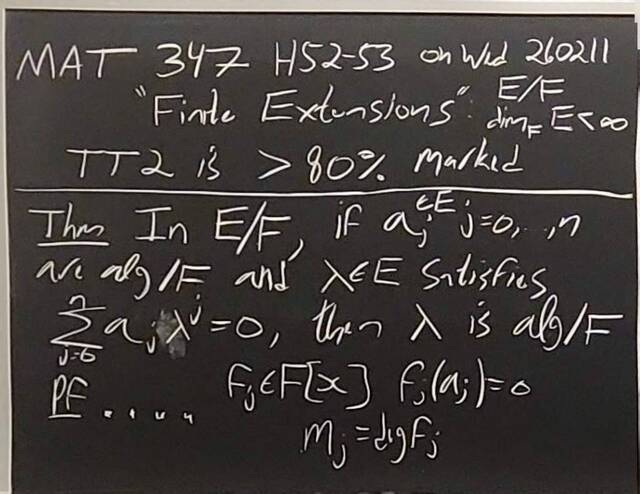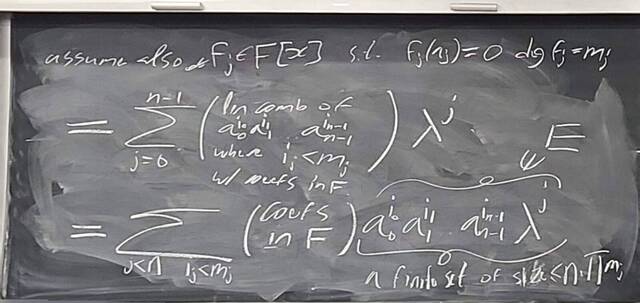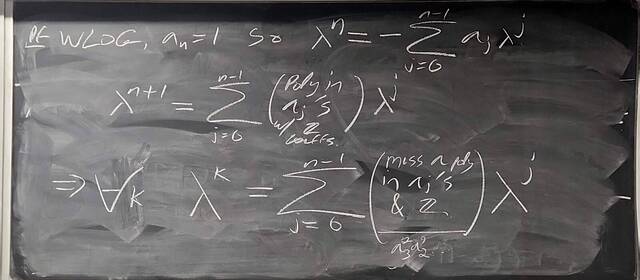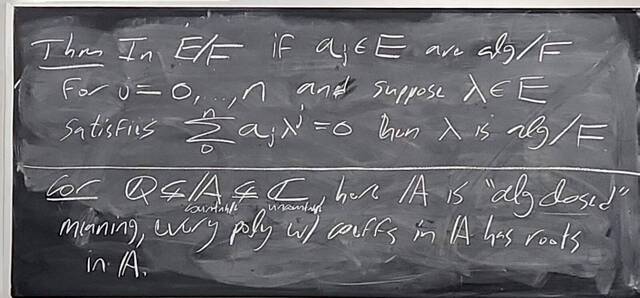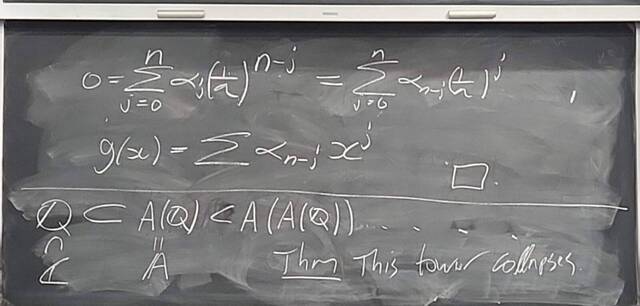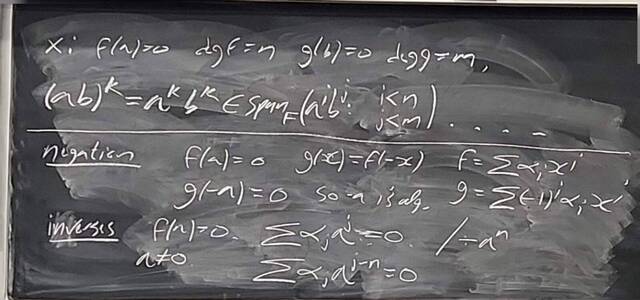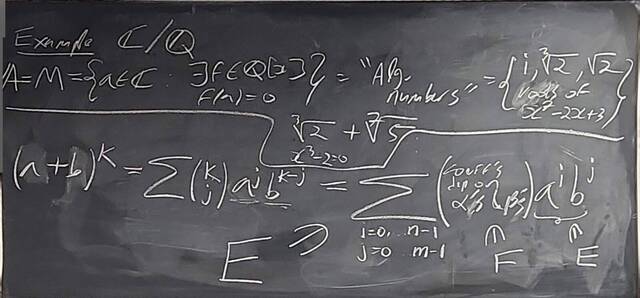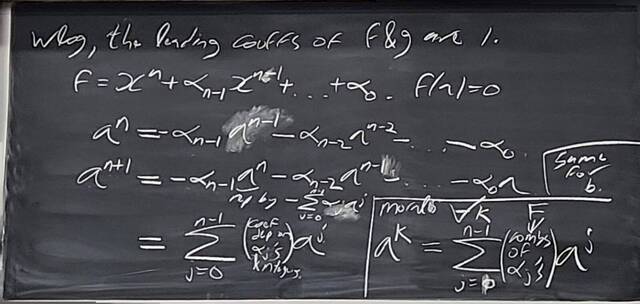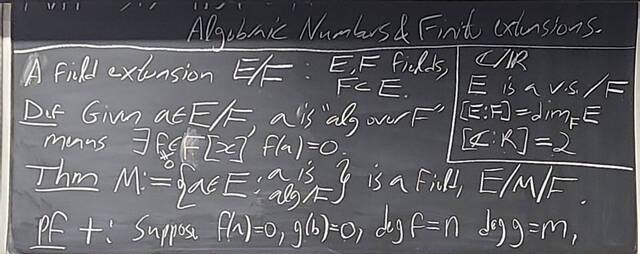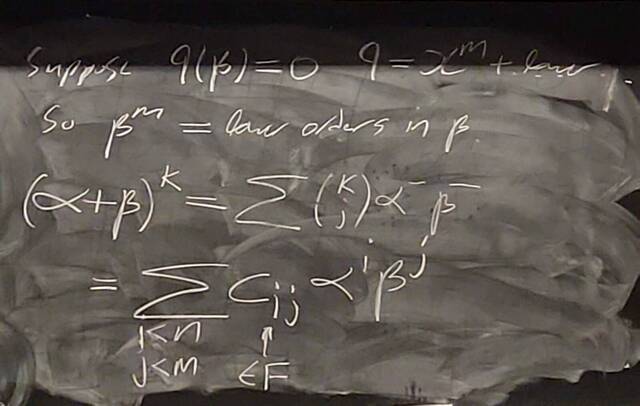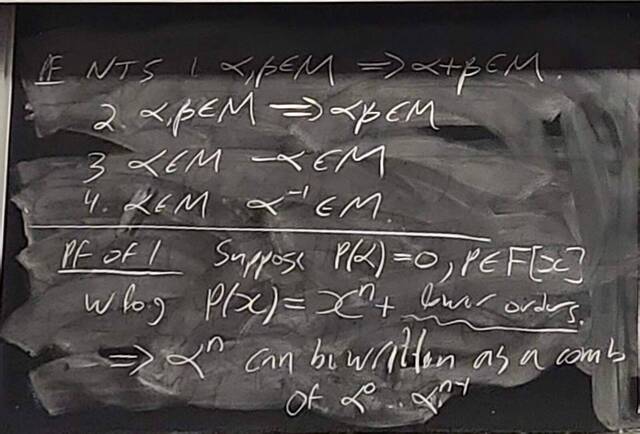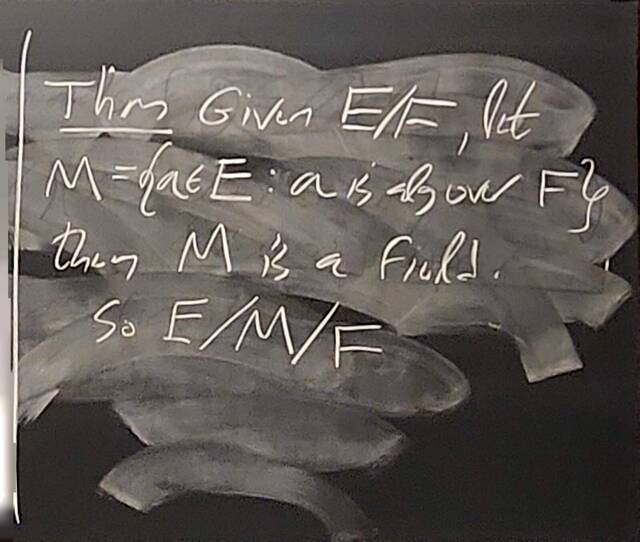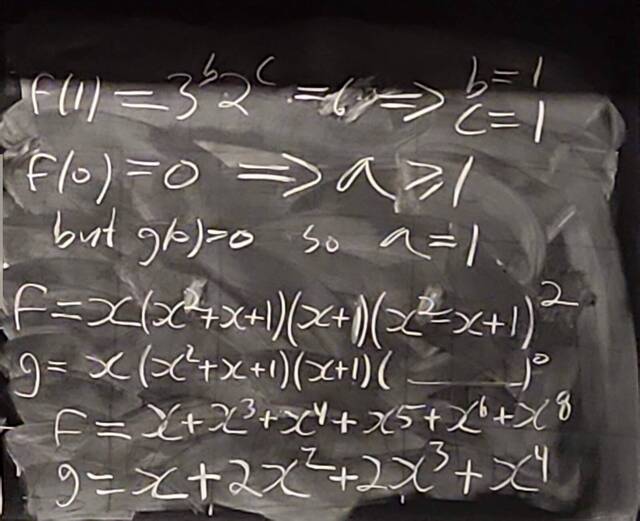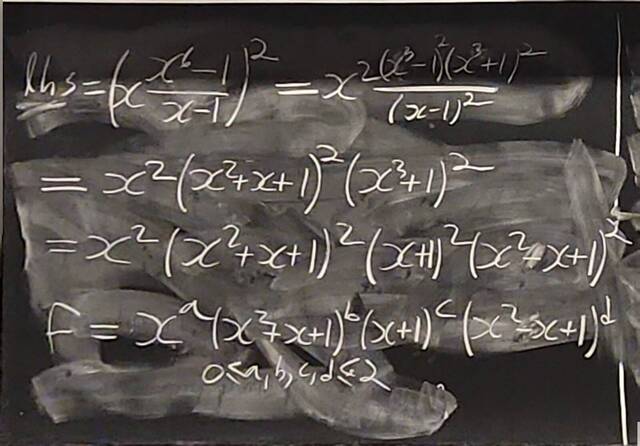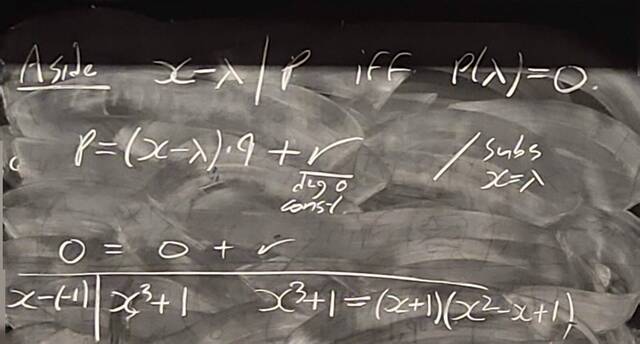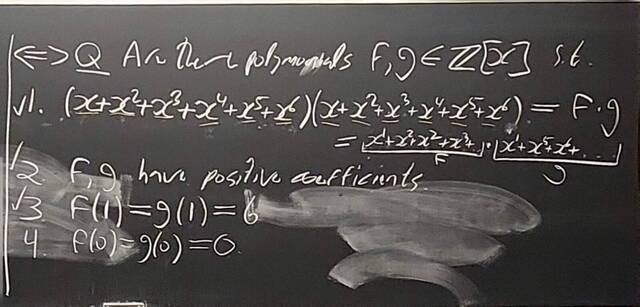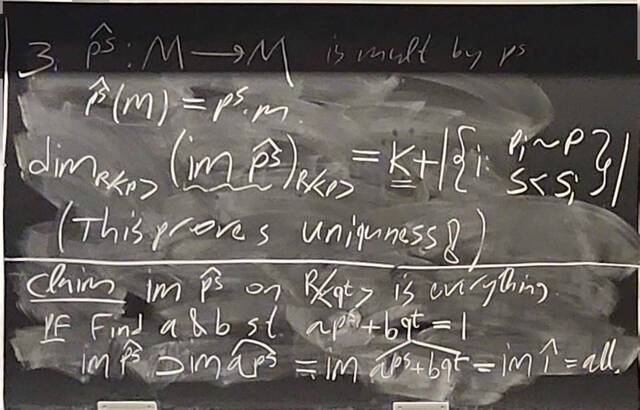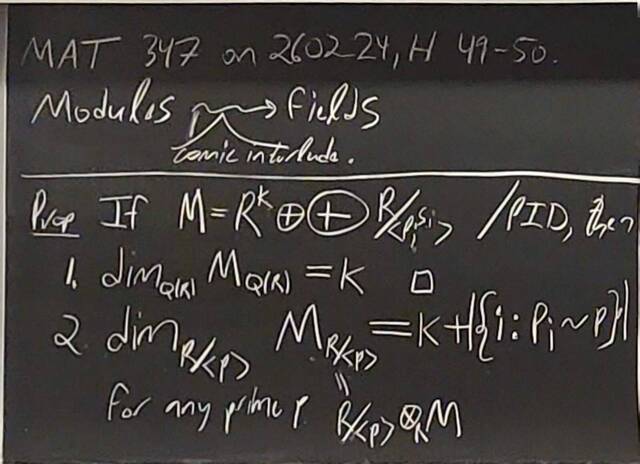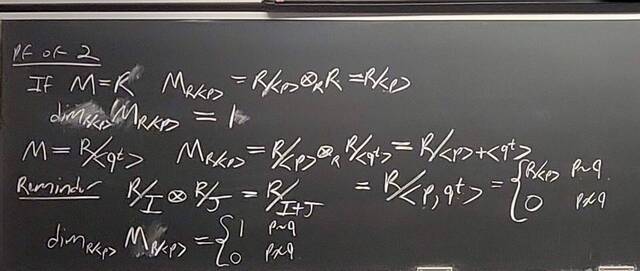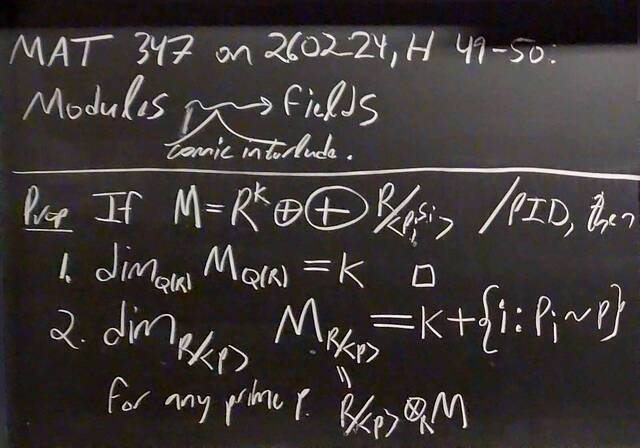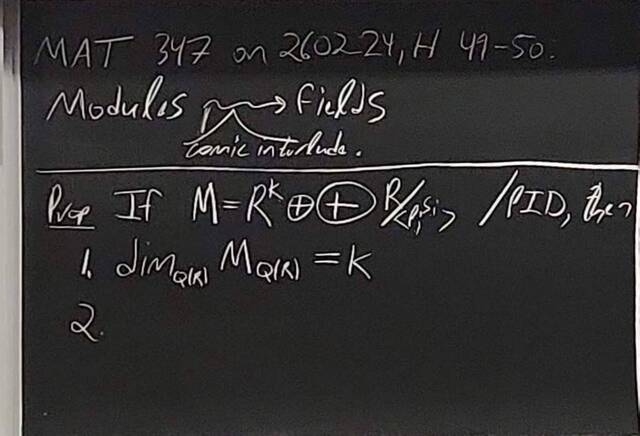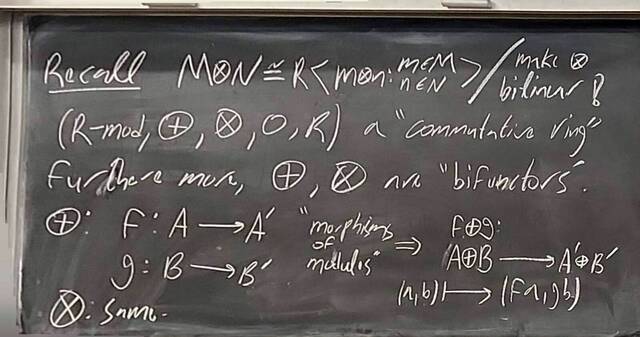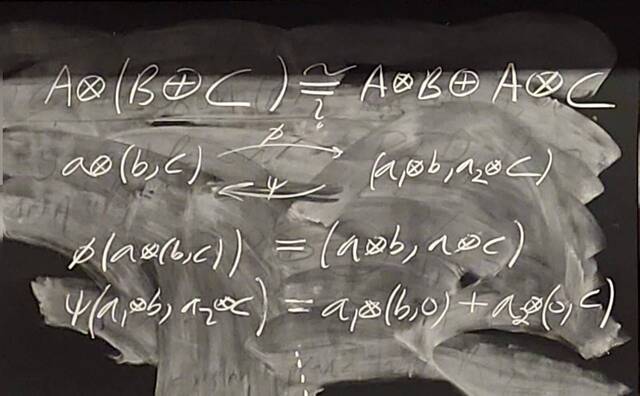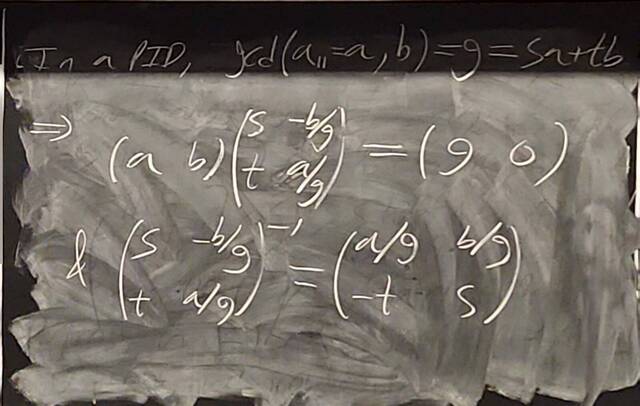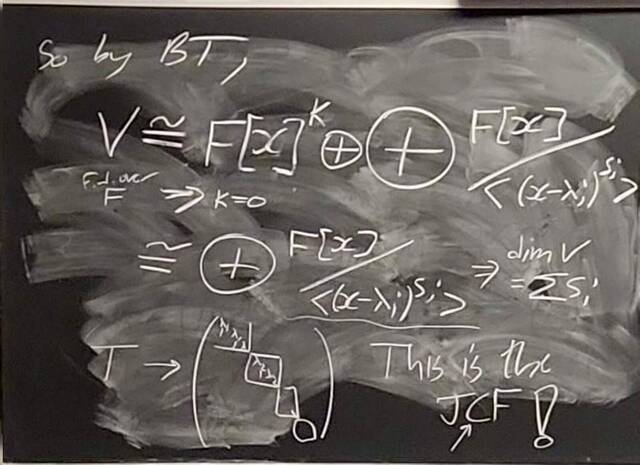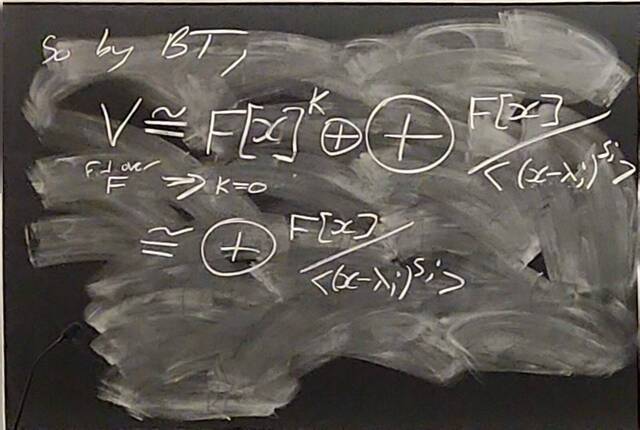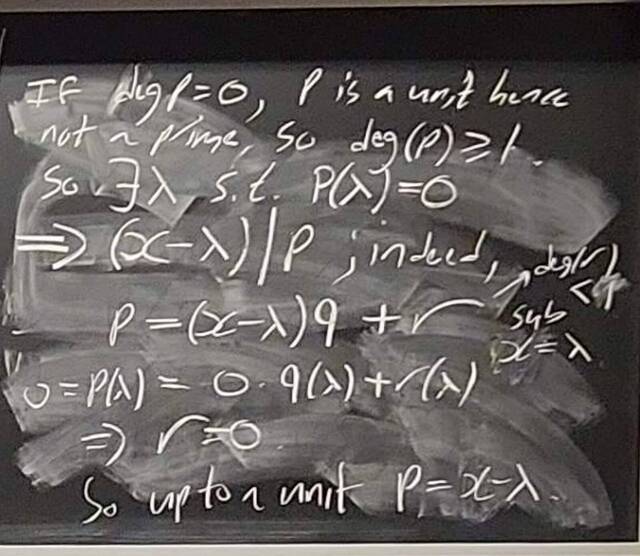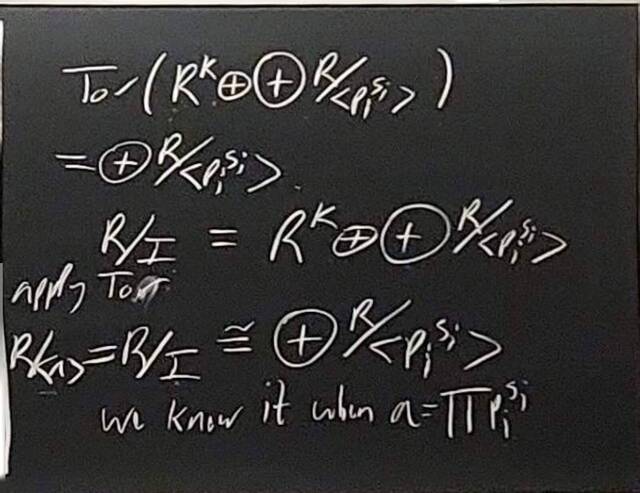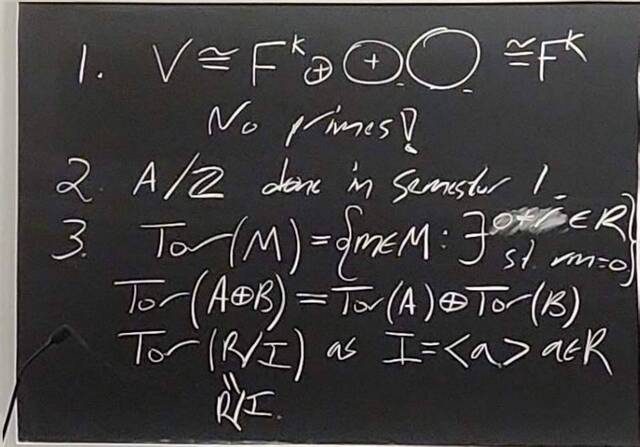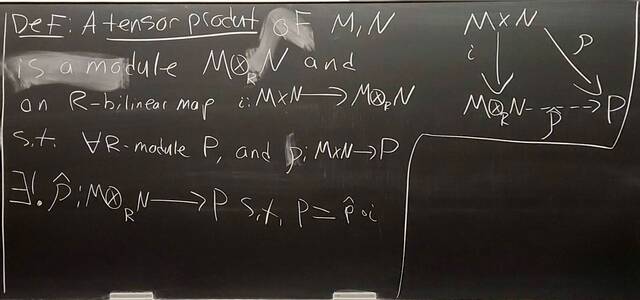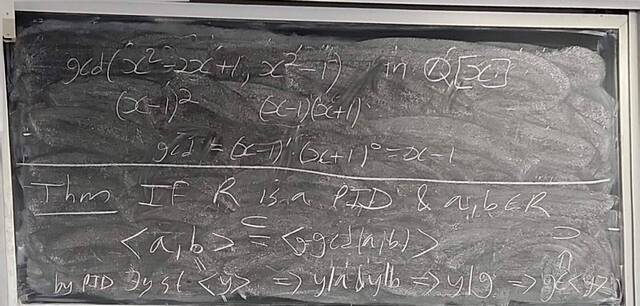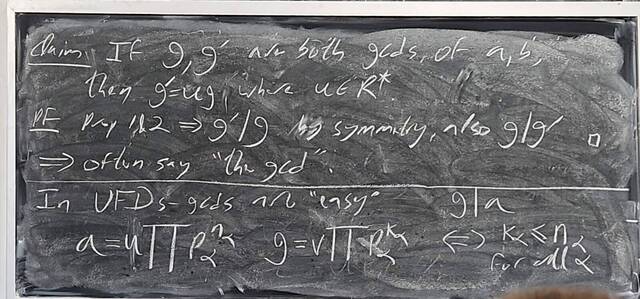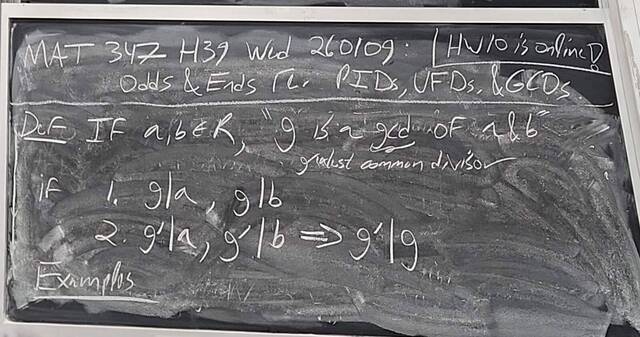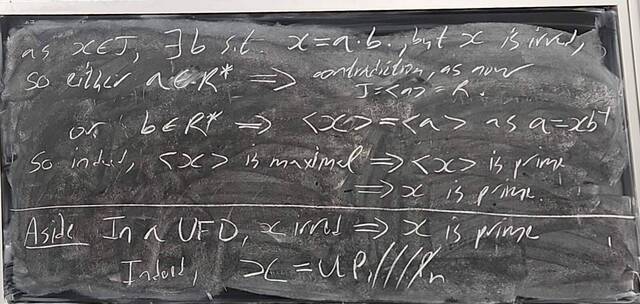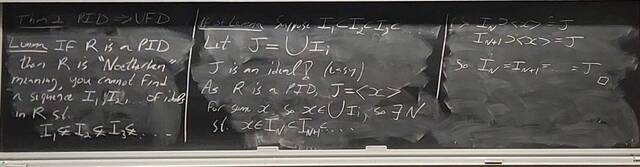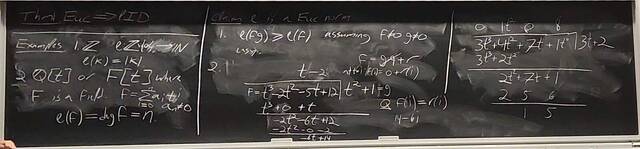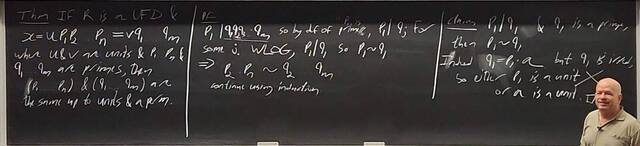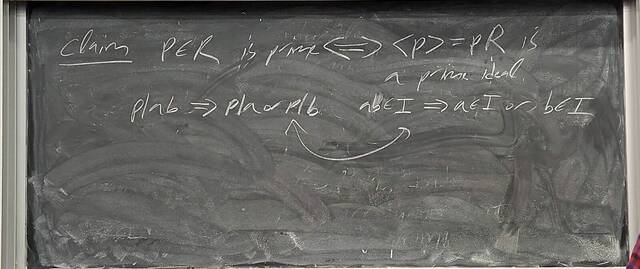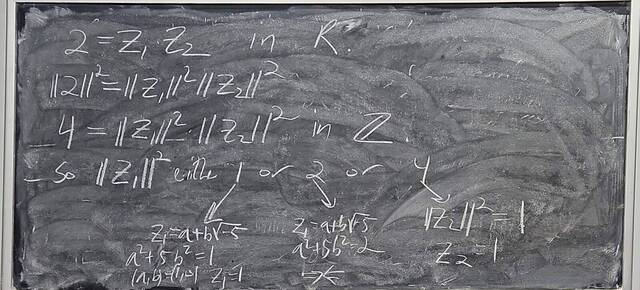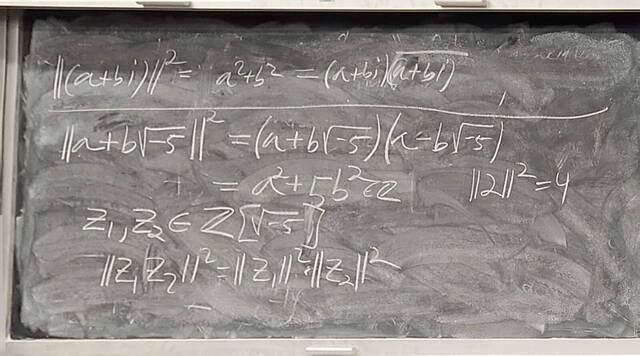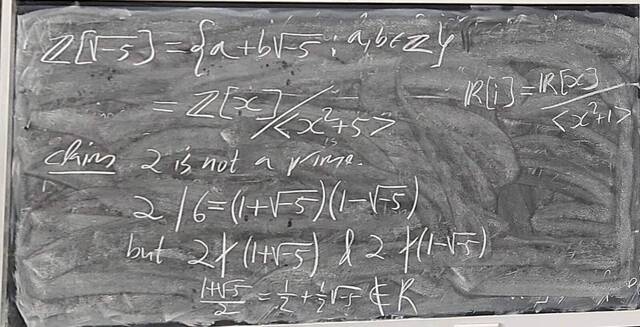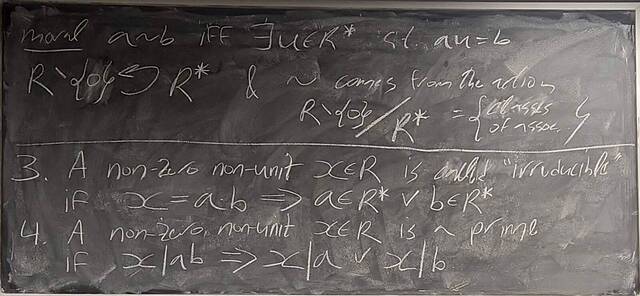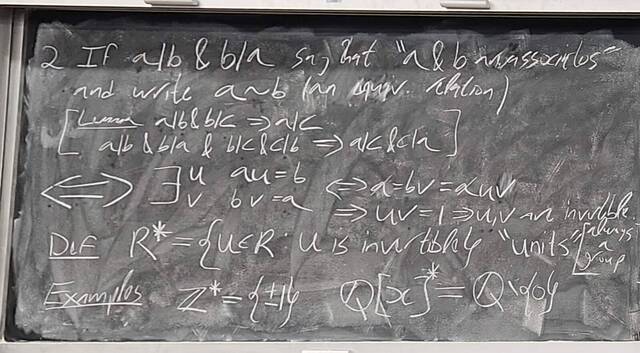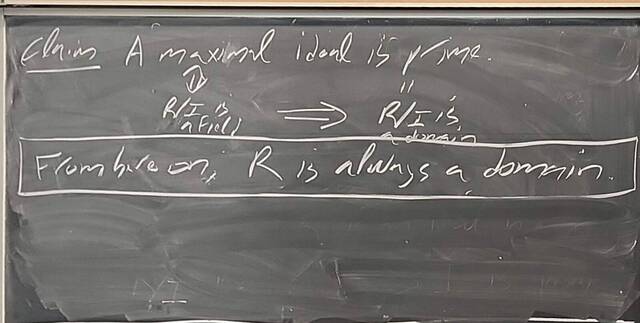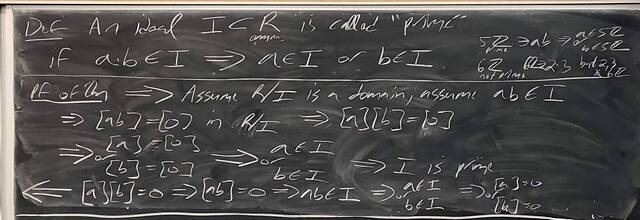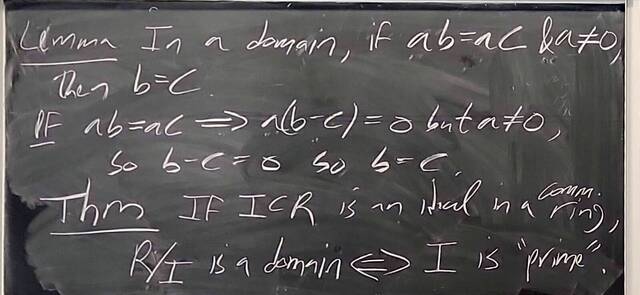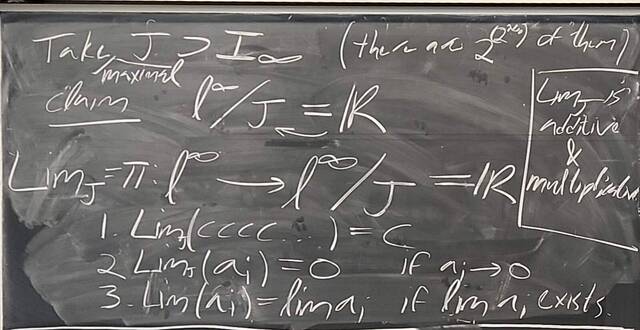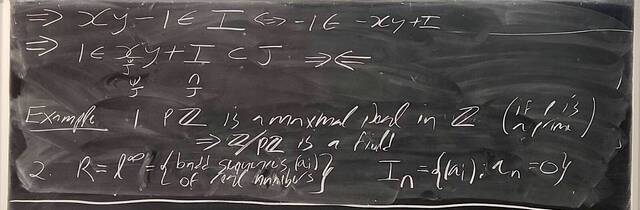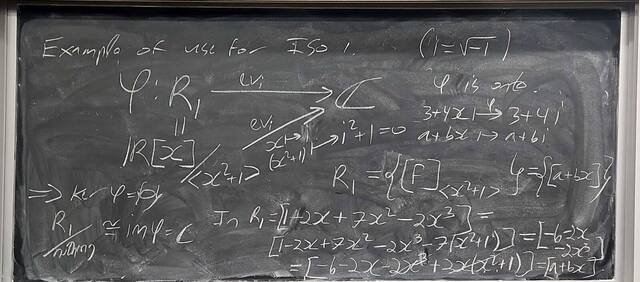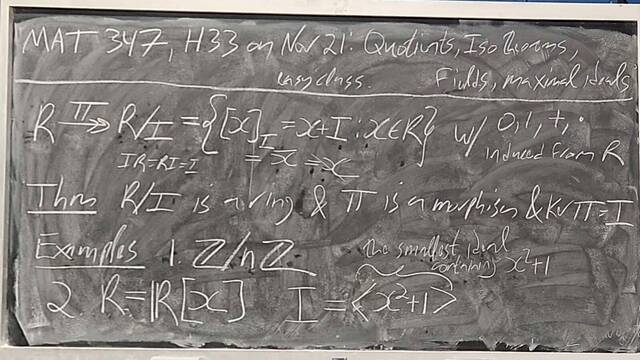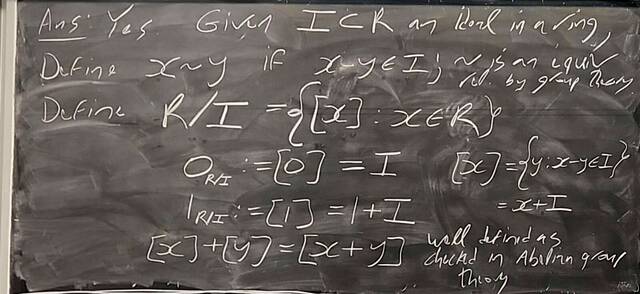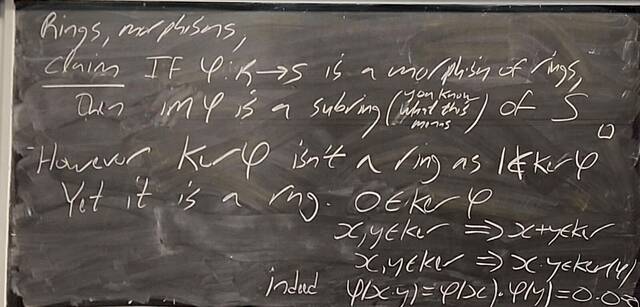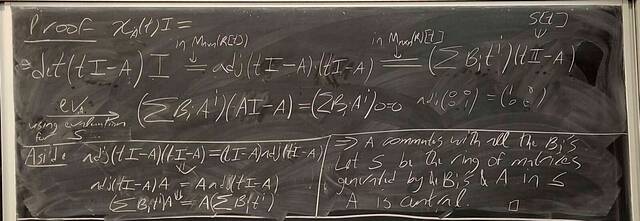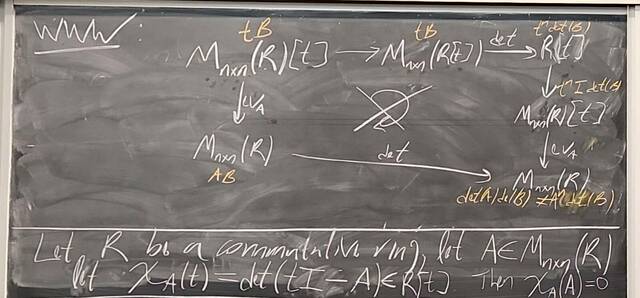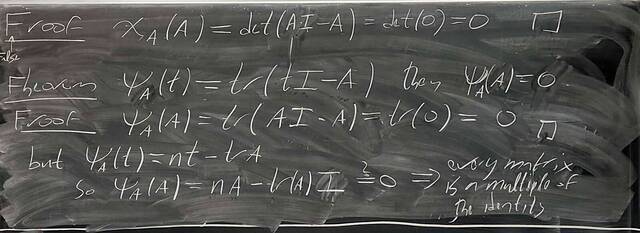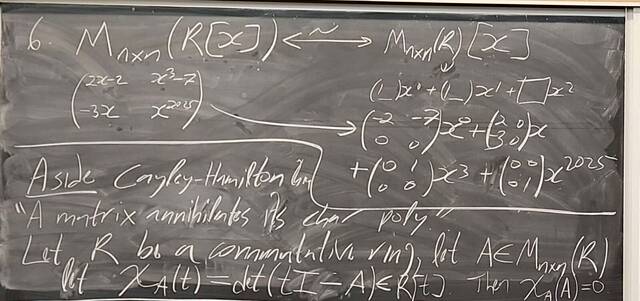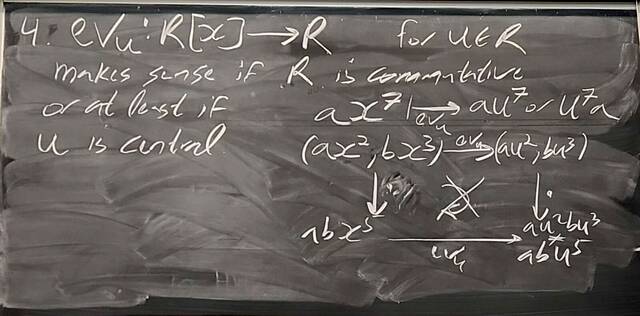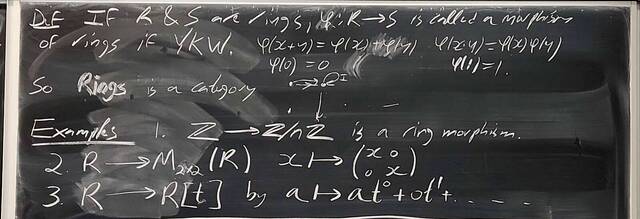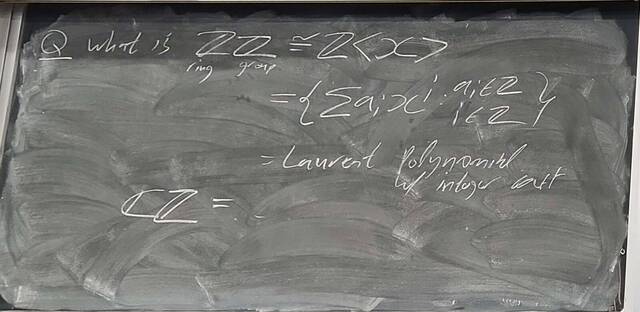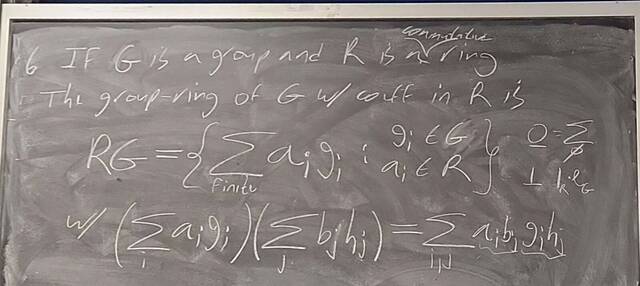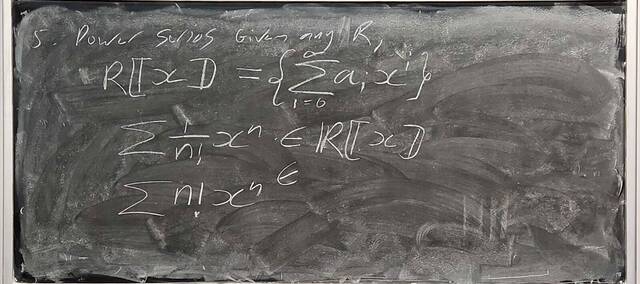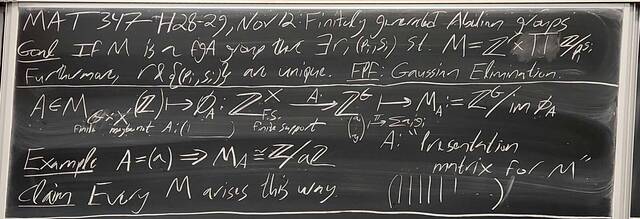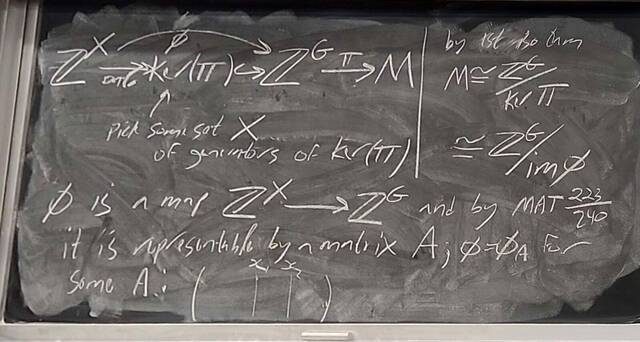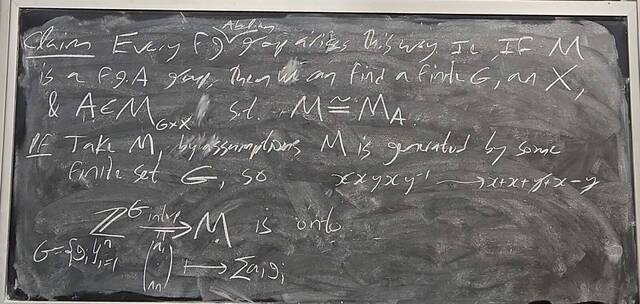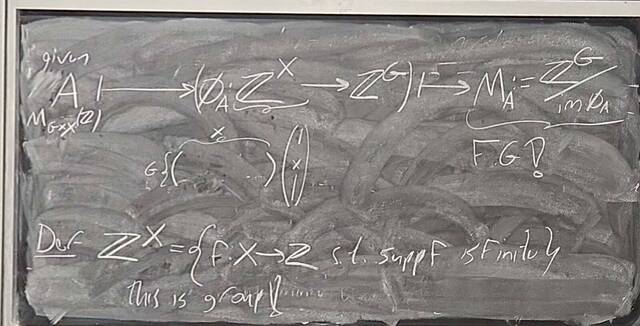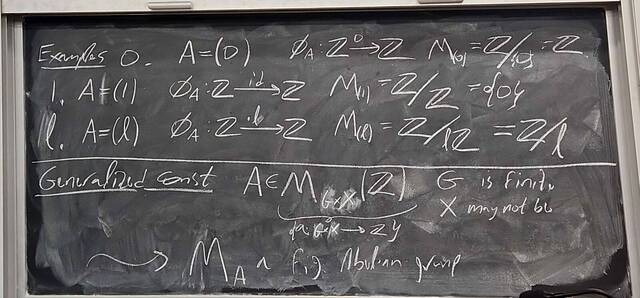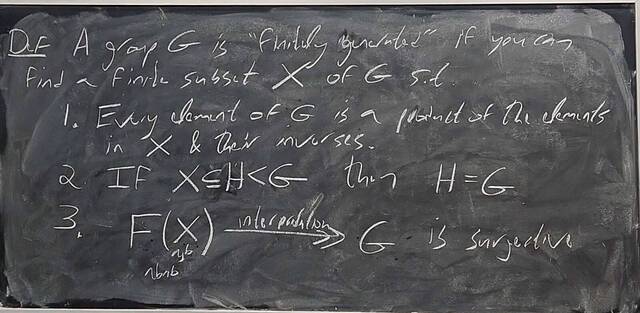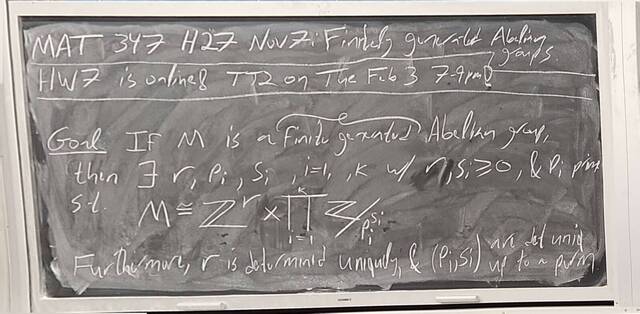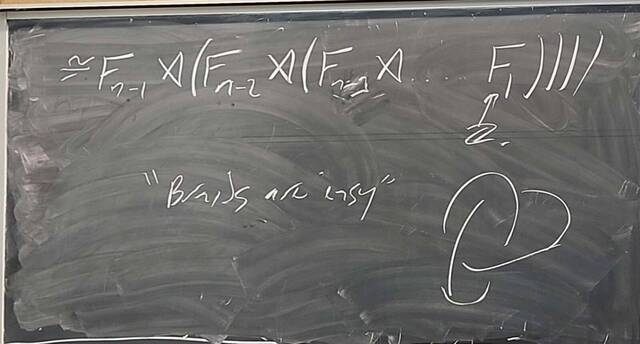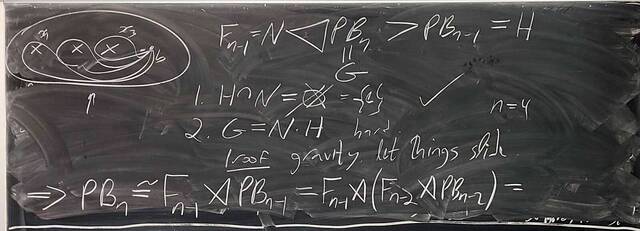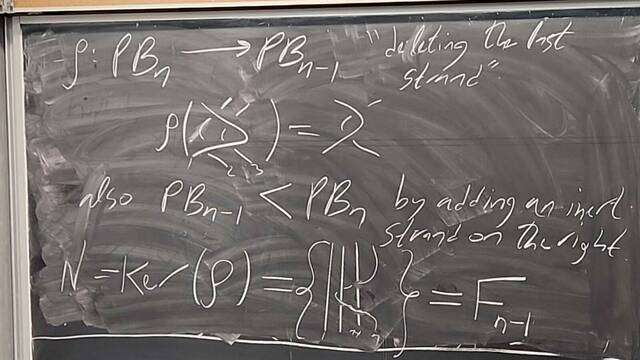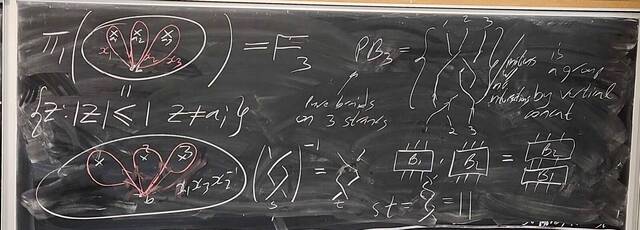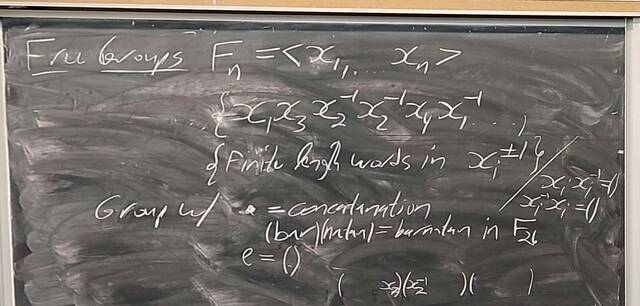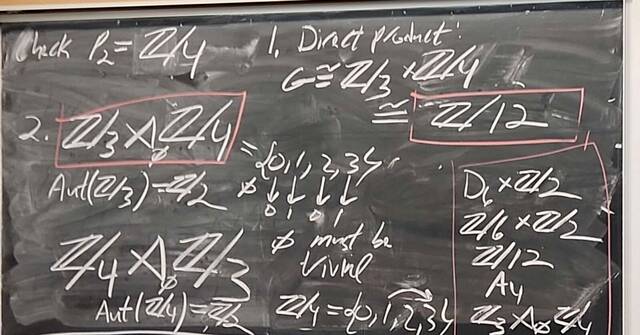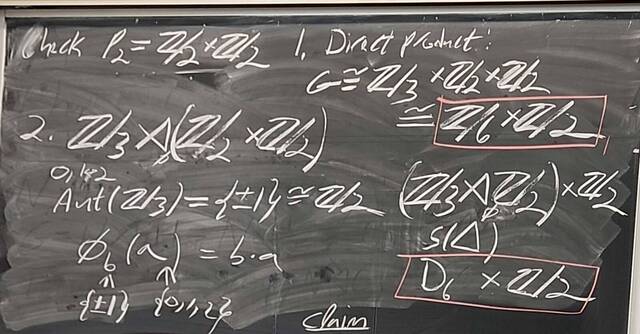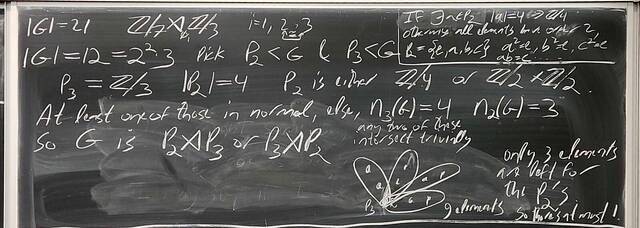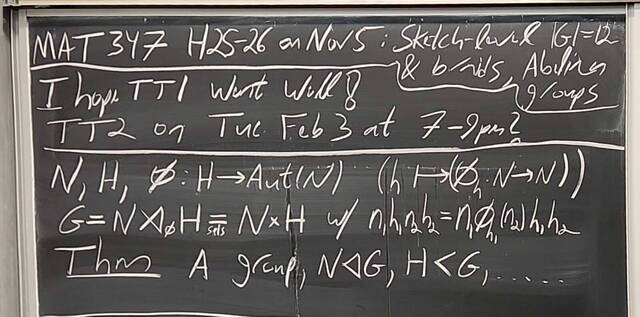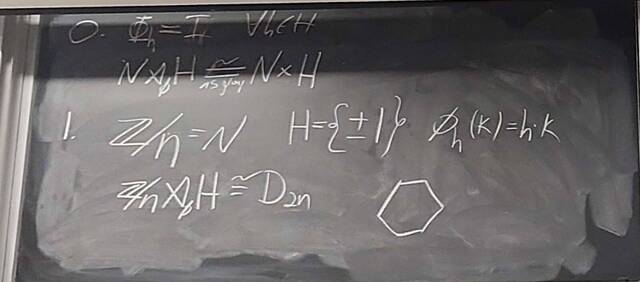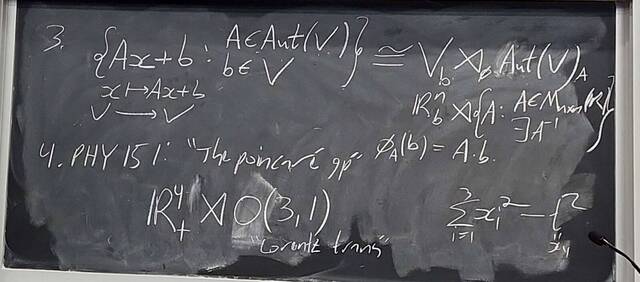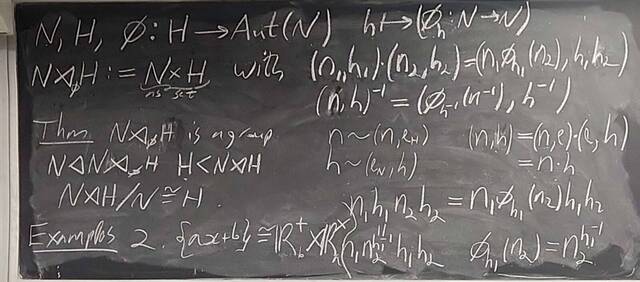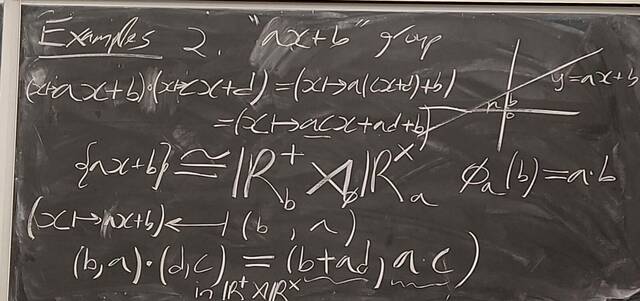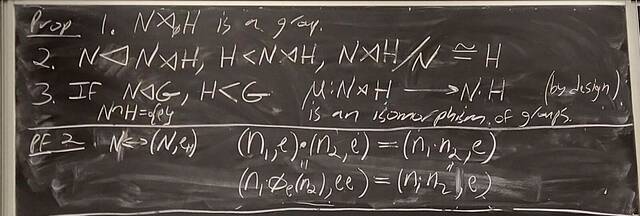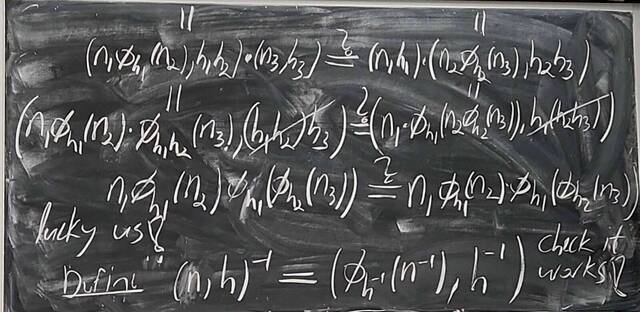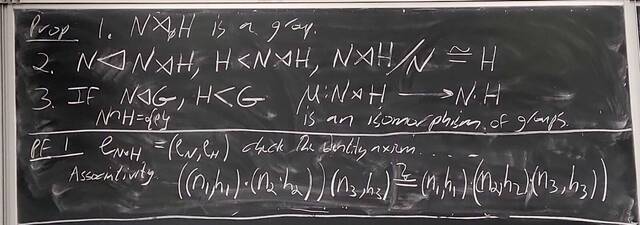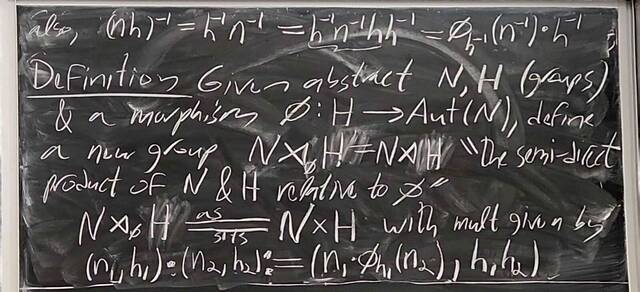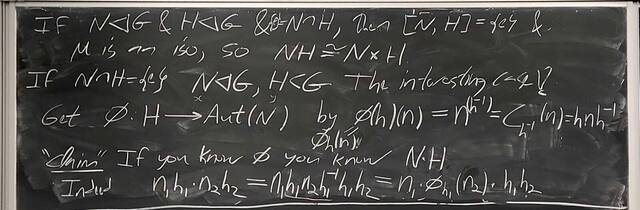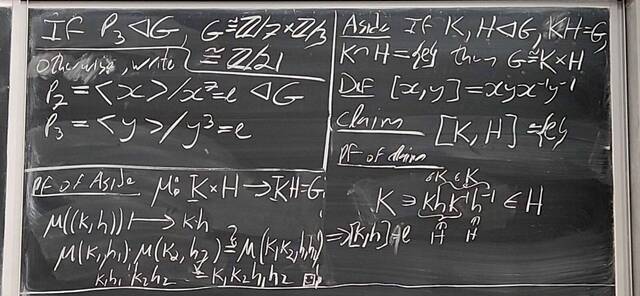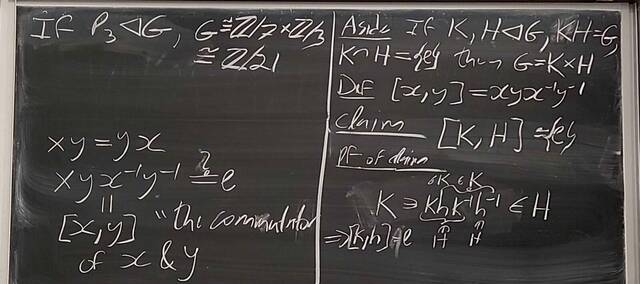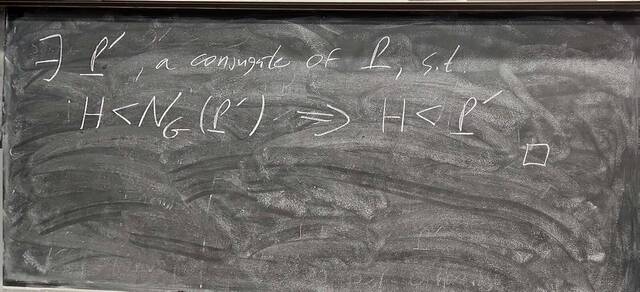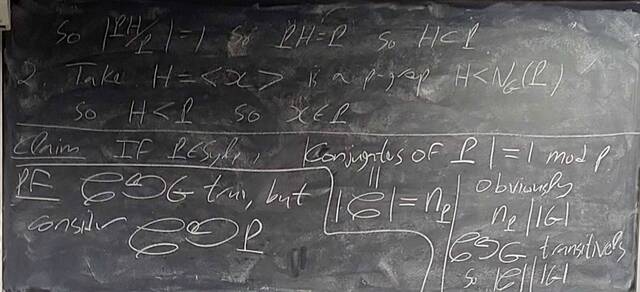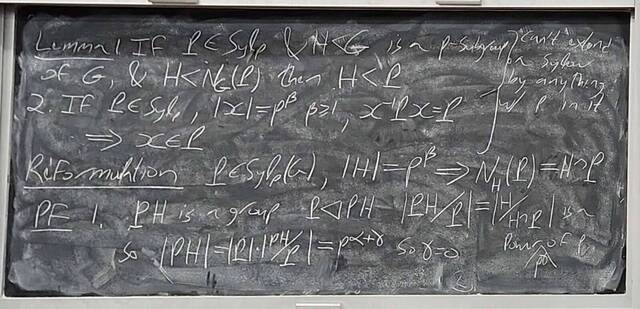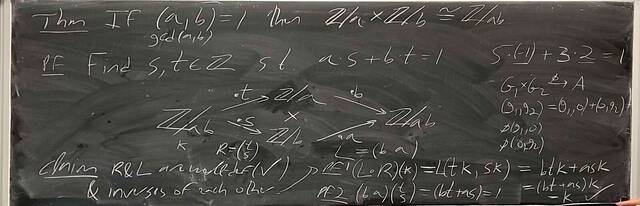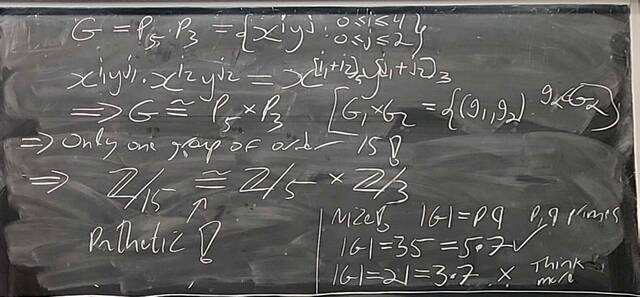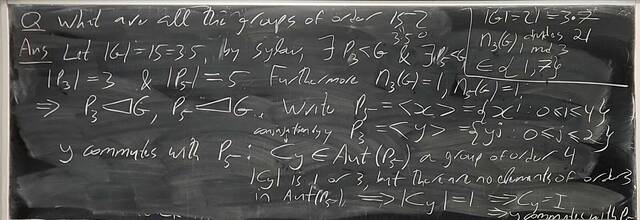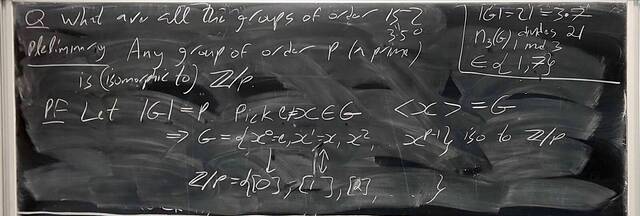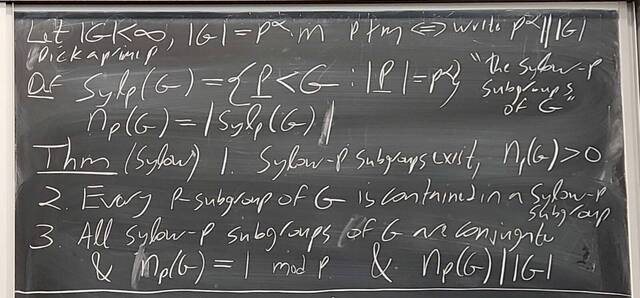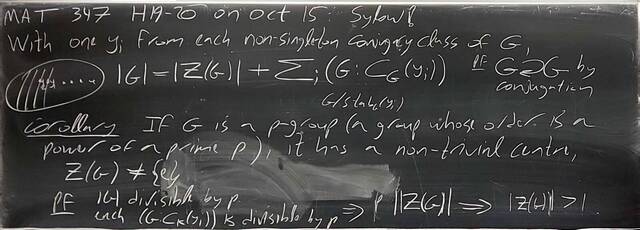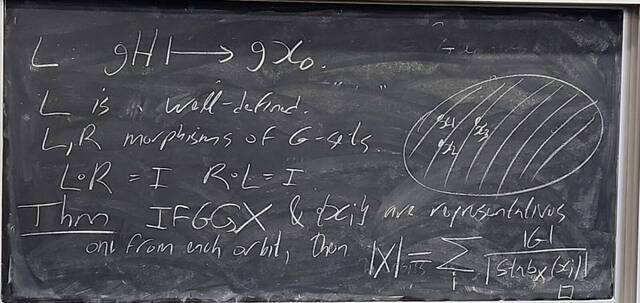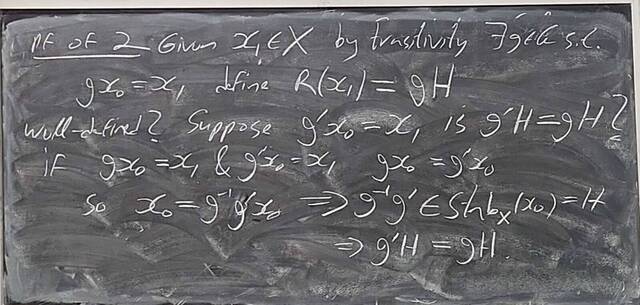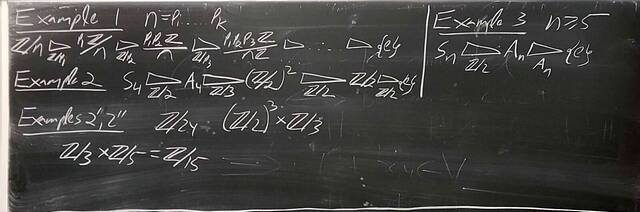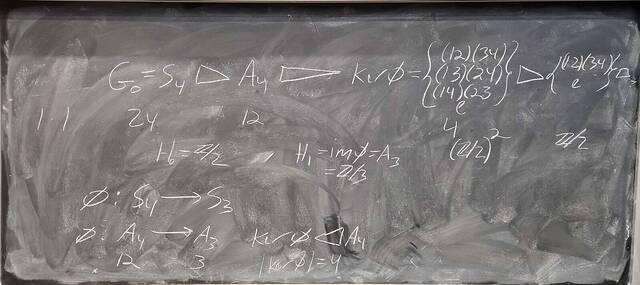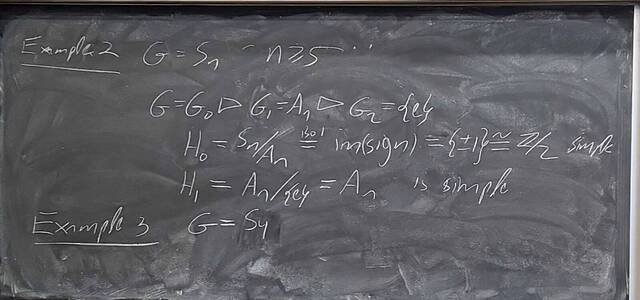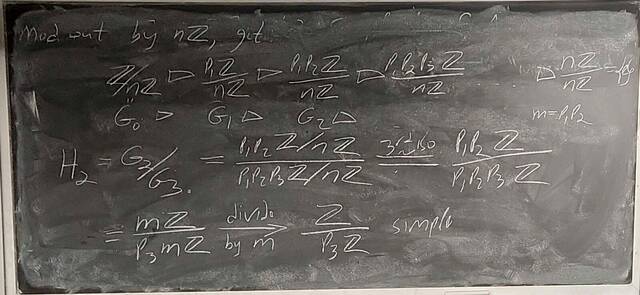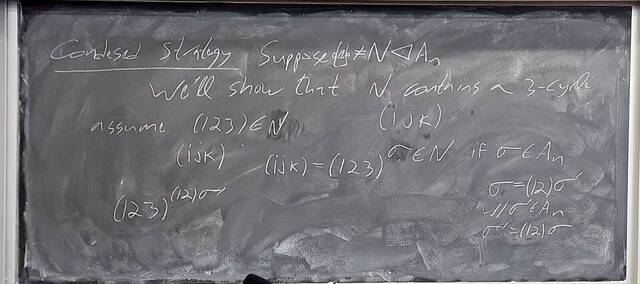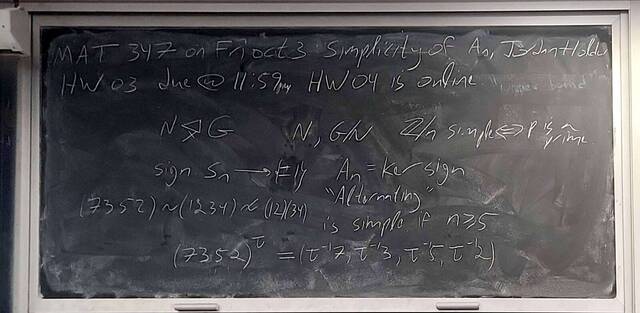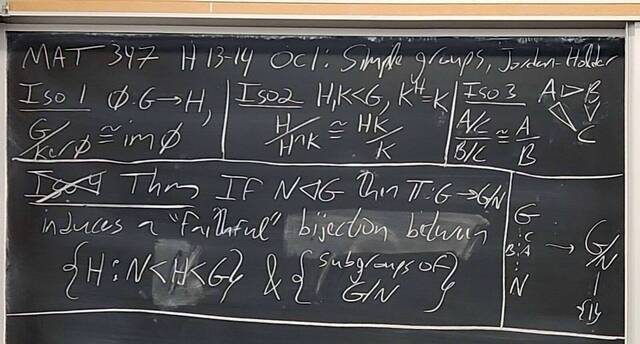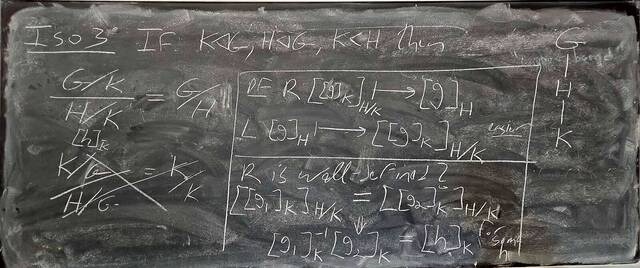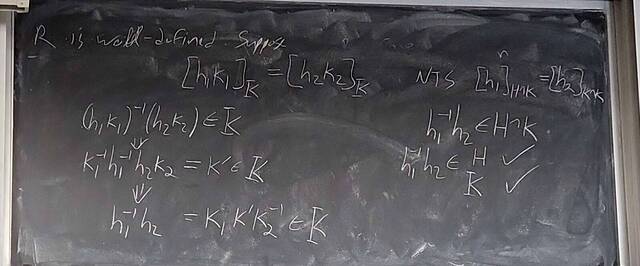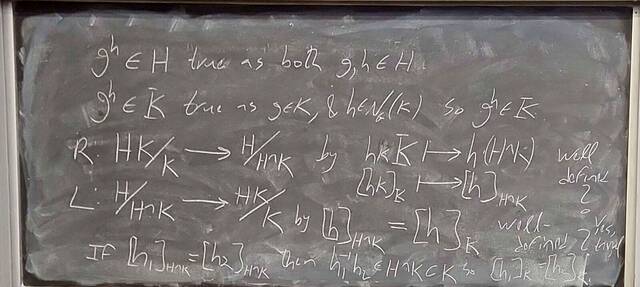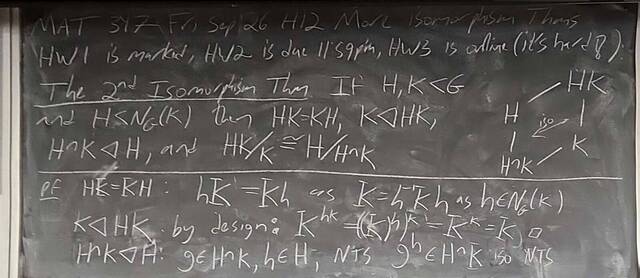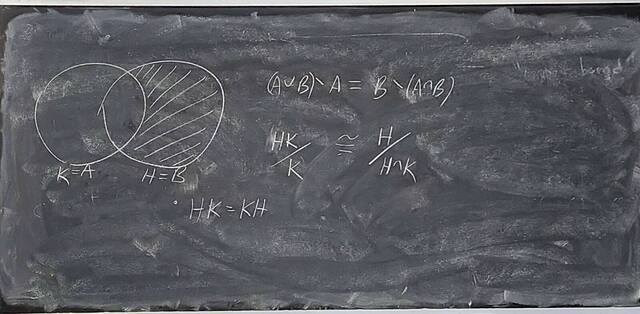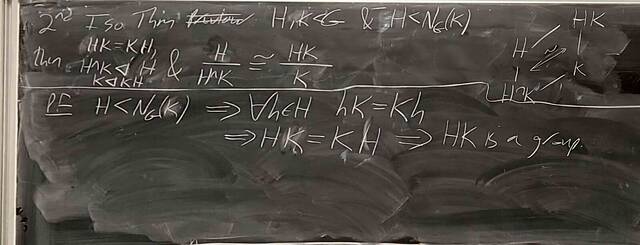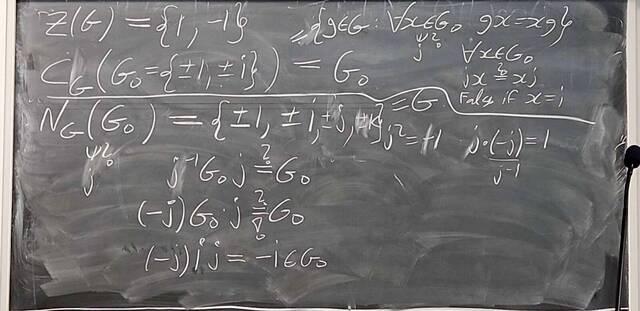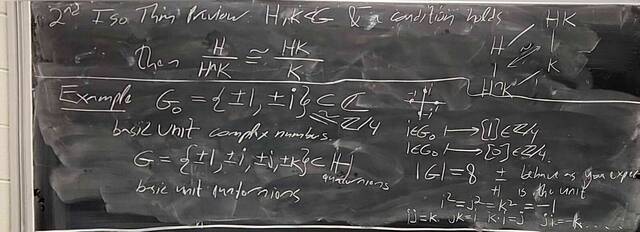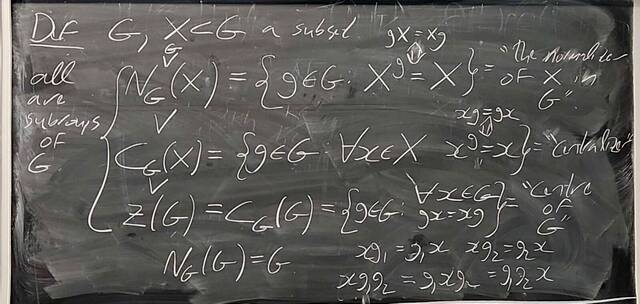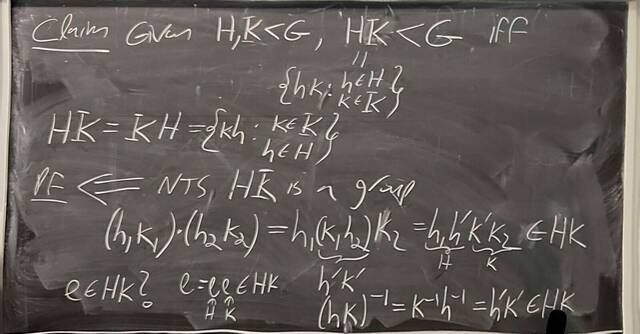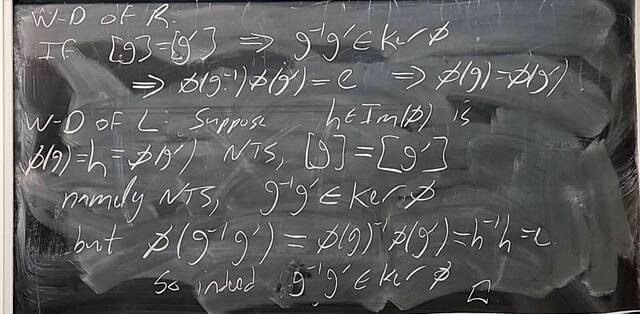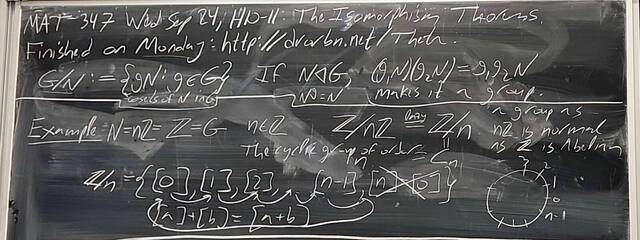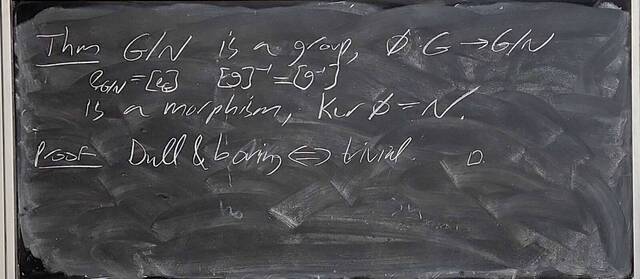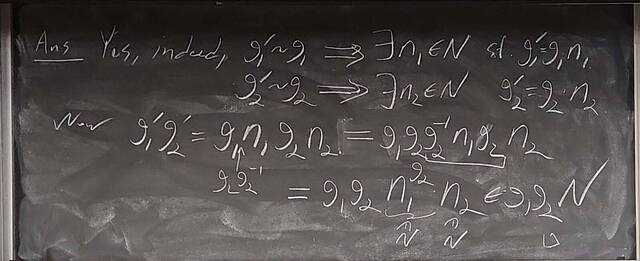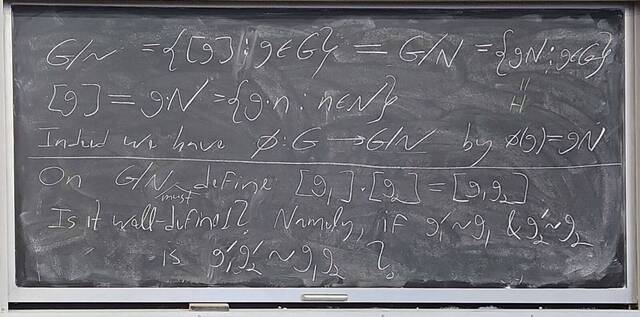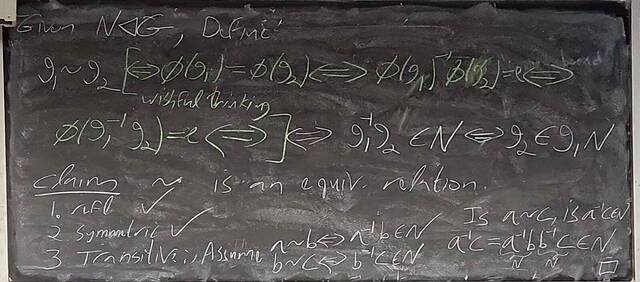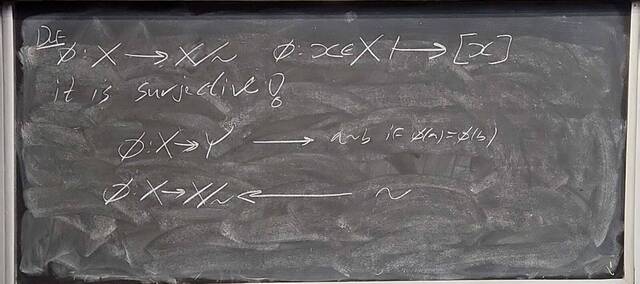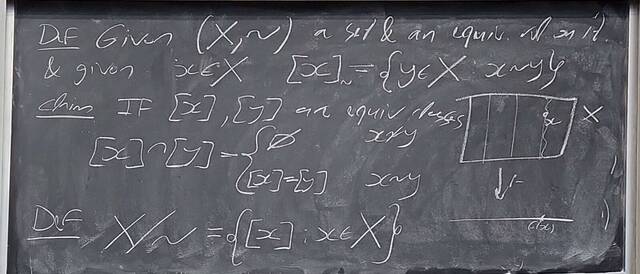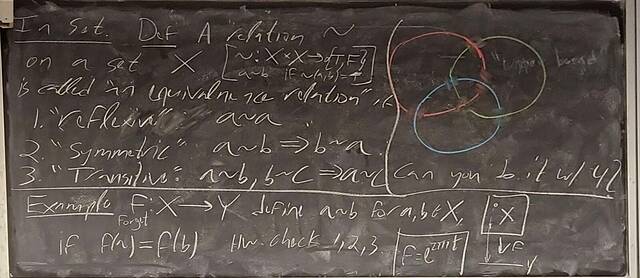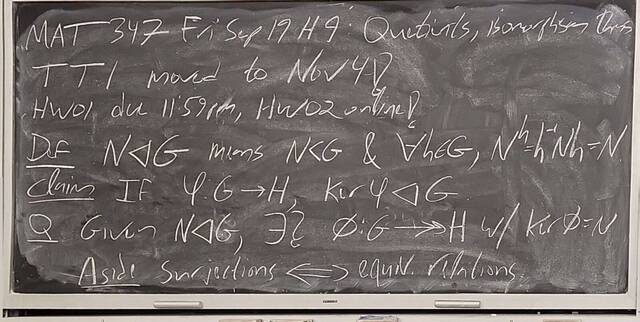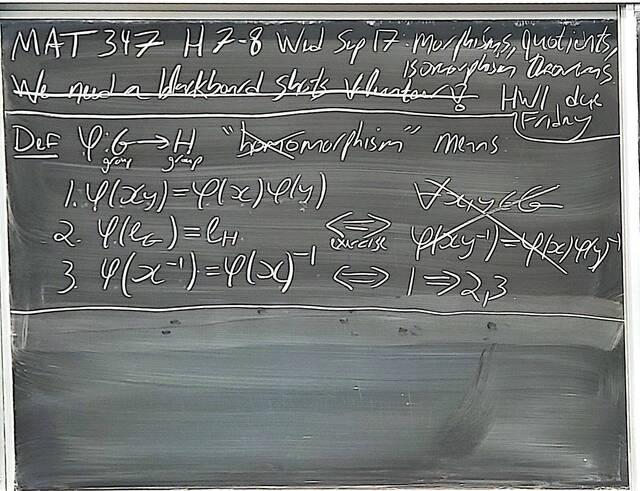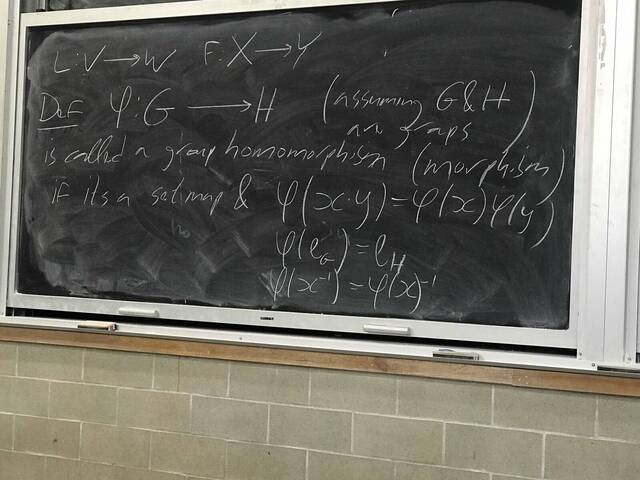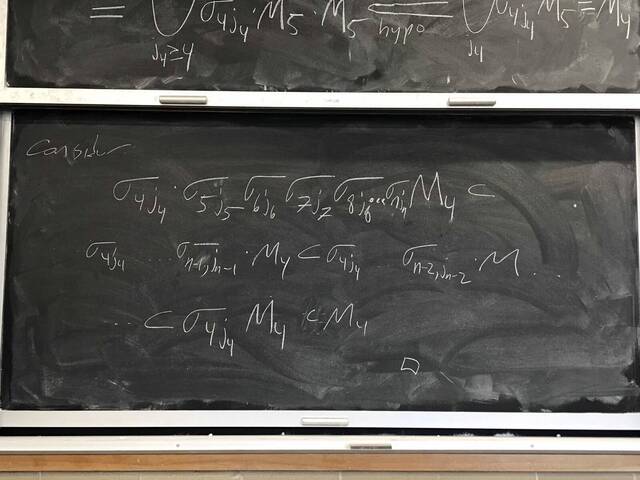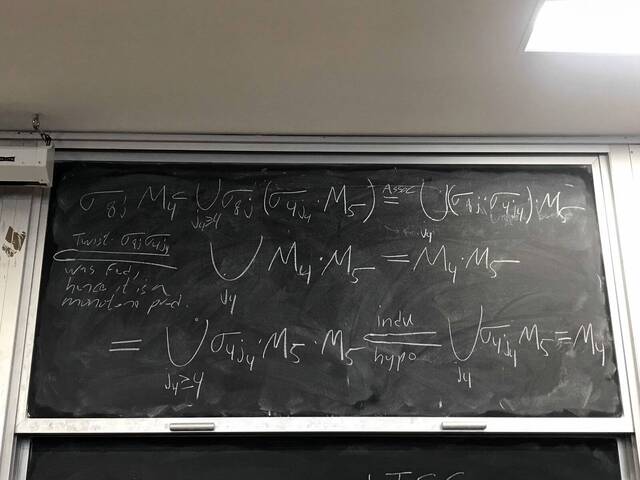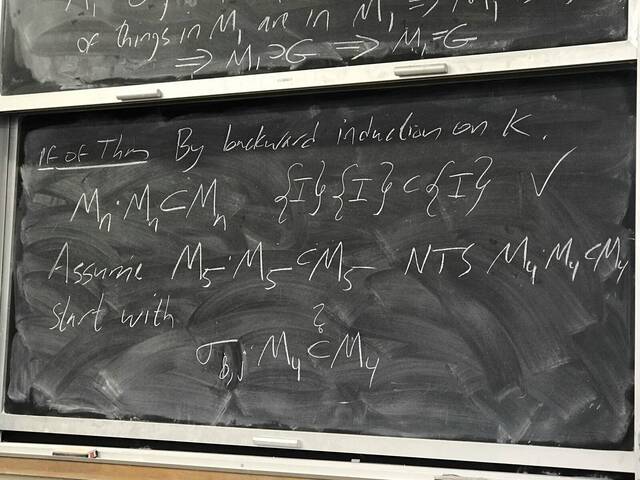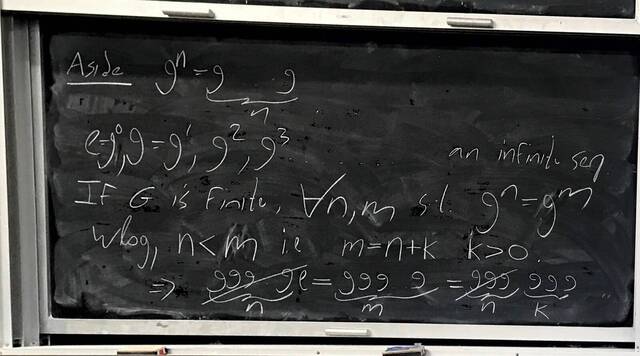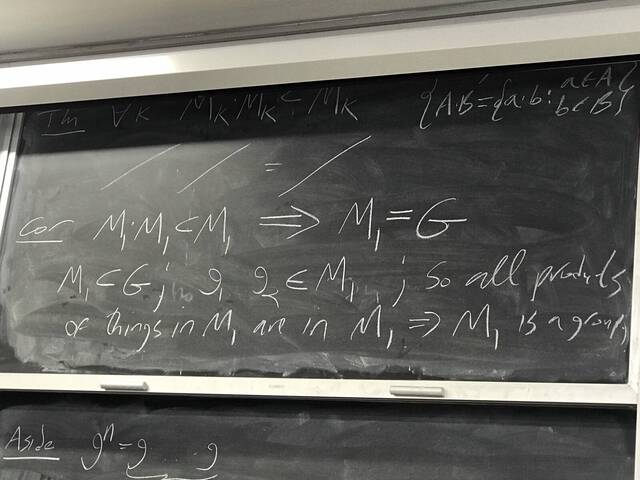Blackboard Shots with Prefix "25-347"
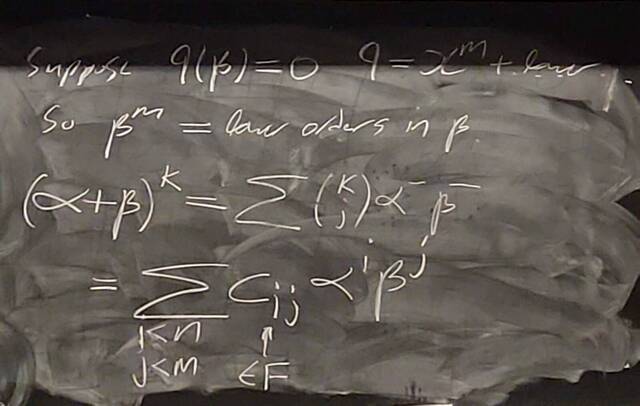 260204-130445
260204-130445: End of modules, the Sicherman dice, algebraic numbers (21).
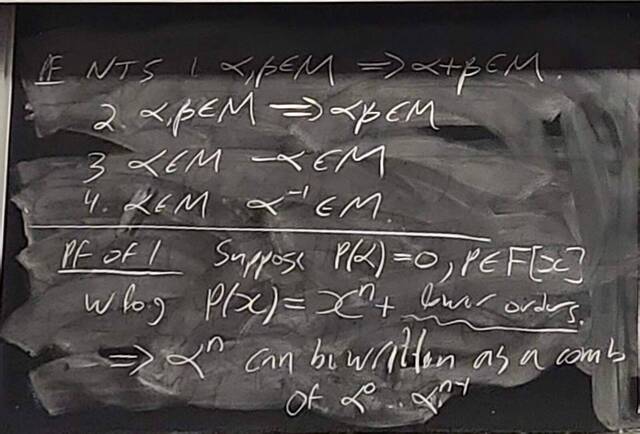 260204-130444
260204-130444: End of modules, the Sicherman dice, algebraic numbers (20).
 260204-130443
260204-130443: End of modules, the Sicherman dice, algebraic numbers (19).
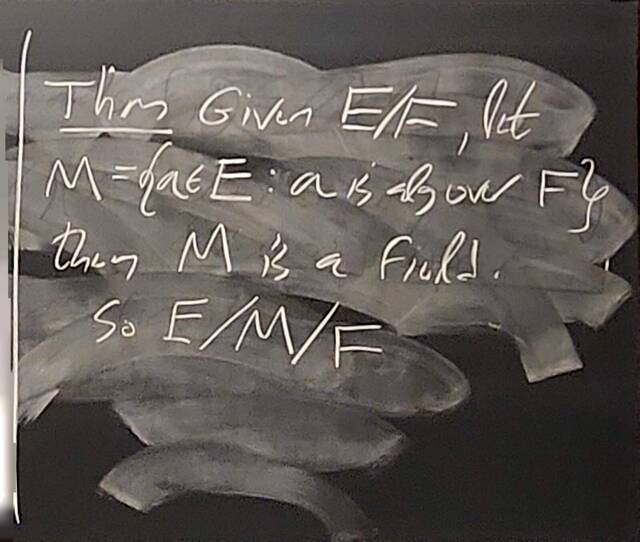 260204-130442
260204-130442: End of modules, the Sicherman dice, algebraic numbers (18).
 260204-130441
260204-130441: End of modules, the Sicherman dice, algebraic numbers (17).
 260204-130440
260204-130440: End of modules, the Sicherman dice, algebraic numbers (16).
 260204-130439
260204-130439: End of modules, the Sicherman dice, algebraic numbers (15).
 260204-130438
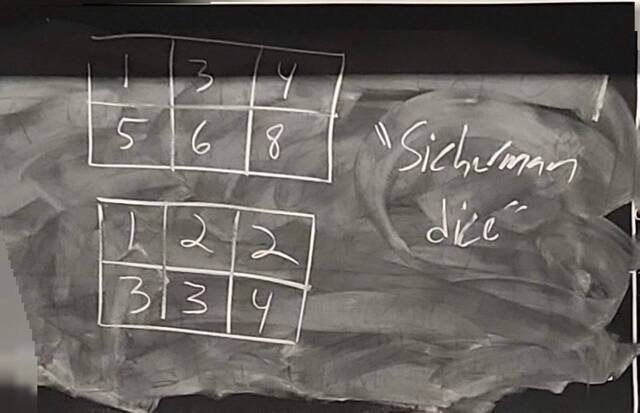
260204-130438: End of modules, the Sicherman dice, algebraic numbers (14).
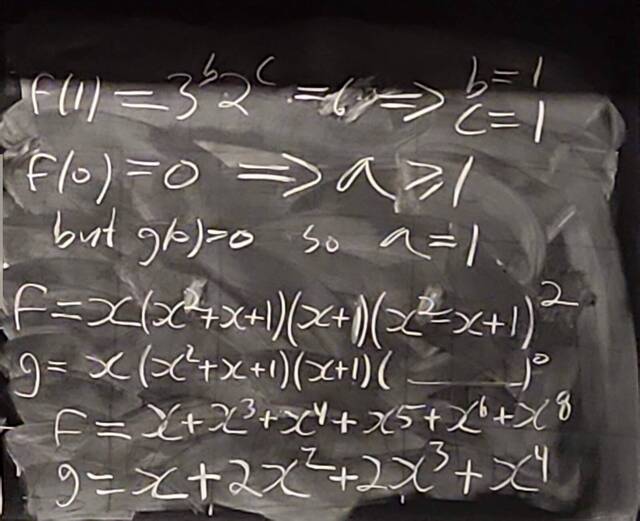 260204-130437
260204-130437: End of modules, the Sicherman dice, algebraic numbers (13).
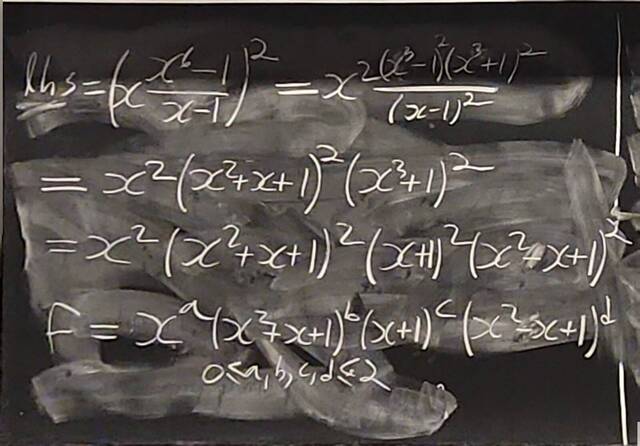 260204-130436
260204-130436: End of modules, the Sicherman dice, algebraic numbers (12).
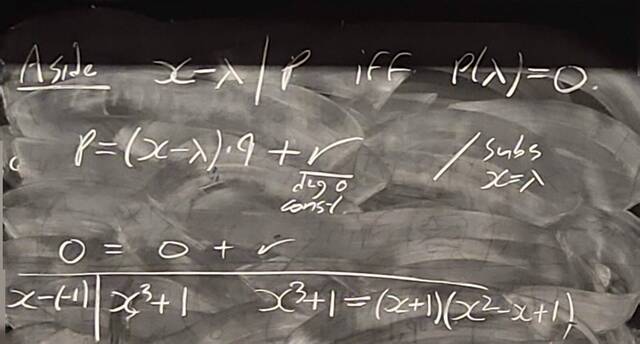 260204-130435
260204-130435: End of modules, the Sicherman dice, algebraic numbers (11).
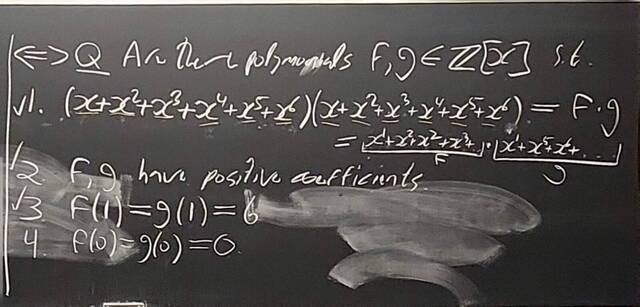 260204-130434
260204-130434: End of modules, the Sicherman dice, algebraic numbers (10).
 260204-130433
260204-130433: End of modules, the Sicherman dice, algebraic numbers (9).
 260204-130432
260204-130432: End of modules, the Sicherman dice, algebraic numbers (8).
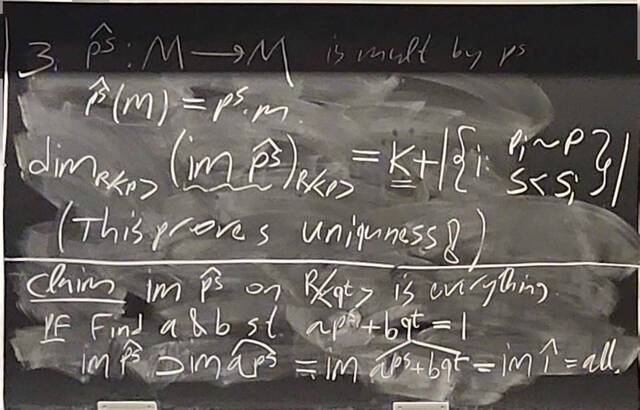 260204-130431
260204-130431: End of modules, the Sicherman dice, algebraic numbers (7).
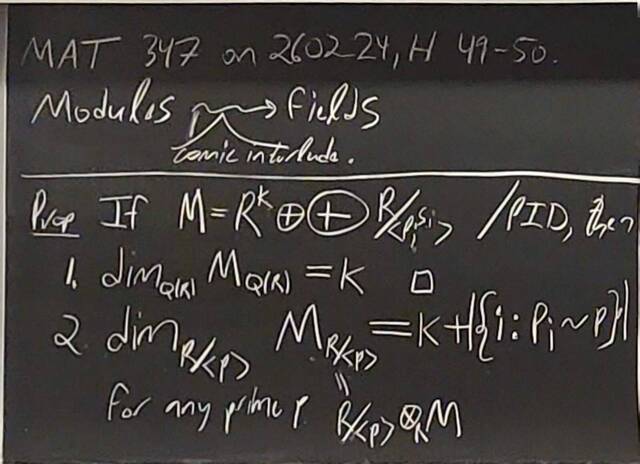 260204-130430
260204-130430: End of modules, the Sicherman dice, algebraic numbers (6).
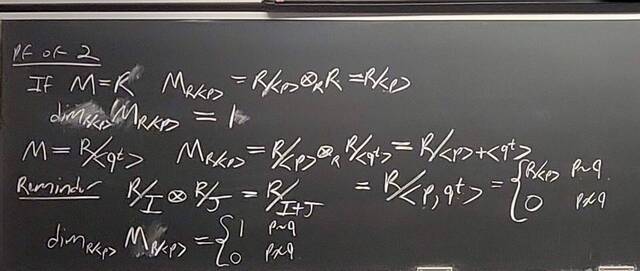 260204-130429
260204-130429: End of modules, the Sicherman dice, algebraic numbers (5).
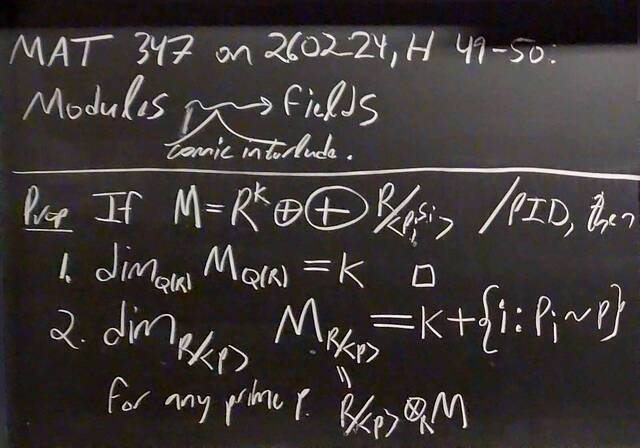 260204-130428
260204-130428: End of modules, the Sicherman dice, algebraic numbers (4).
 260204-130427
260204-130427: End of modules, the Sicherman dice, algebraic numbers (3).
 260204-130426
260204-130426: End of modules, the Sicherman dice, algebraic numbers (2).
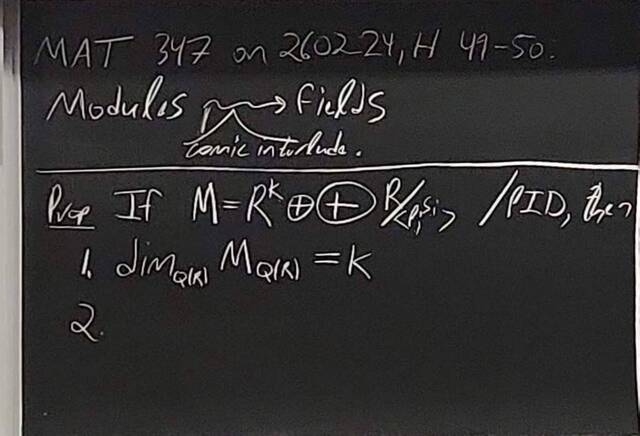 260204-130425
260204-130425: End of modules, the Sicherman dice, algebraic numbers.
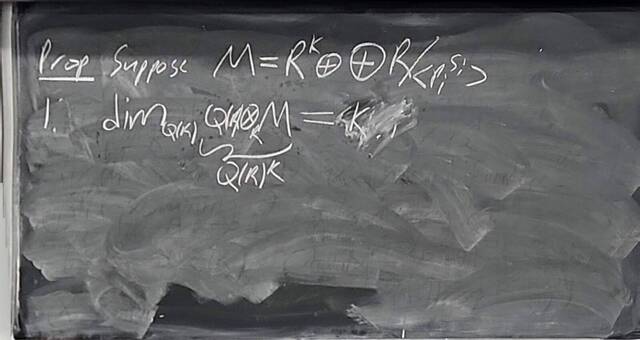 260130-144932
260130-144932: The structure theorem of modules: Towards uniqueness (9).
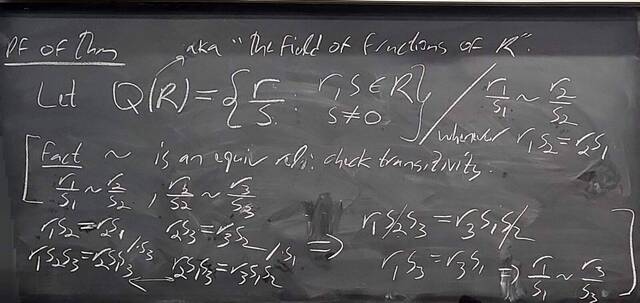 260130-144931
260130-144931: The structure theorem of modules: Towards uniqueness (8).
 260130-144930
260130-144930: The structure theorem of modules: Towards uniqueness (7).
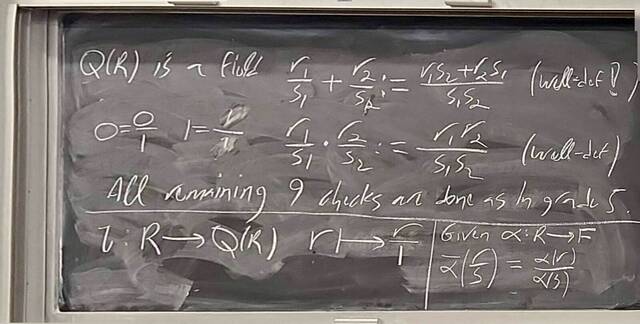 260130-144929
260130-144929: The structure theorem of modules: Towards uniqueness (6).
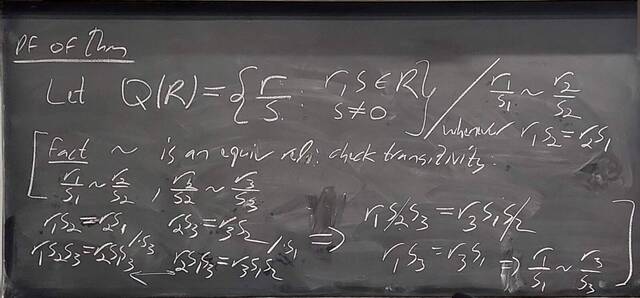 260130-144928
260130-144928: The structure theorem of modules: Towards uniqueness (5).
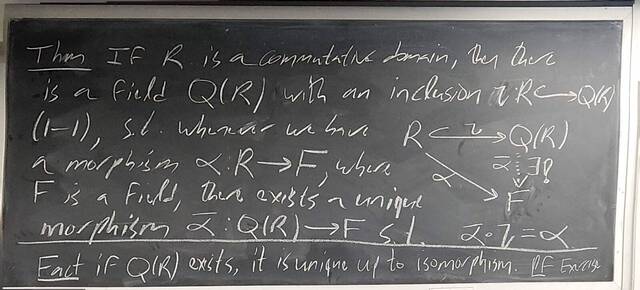 260130-144927
260130-144927: The structure theorem of modules: Towards uniqueness (4).
 260130-144926
260130-144926: The structure theorem of modules: Towards uniqueness (3).
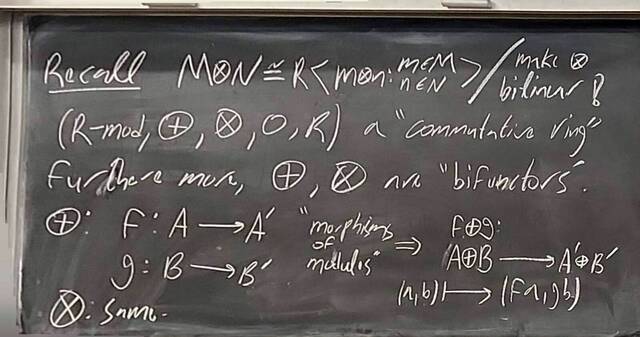 260130-144925
260130-144925: The structure theorem of modules: Towards uniqueness (2).
 260130-144924
260130-144924: The structure theorem of modules: Towards uniqueness.
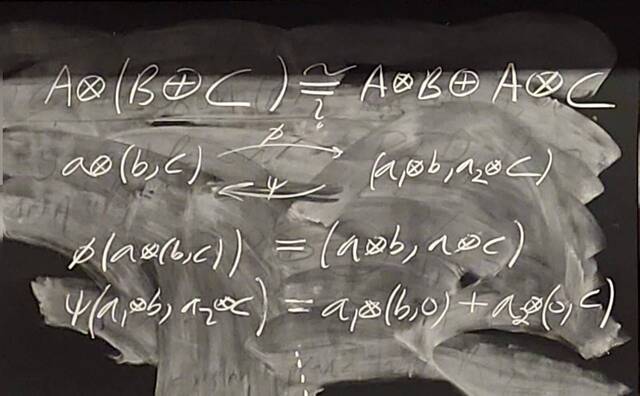 260128-161105
260128-161105: The structure theorem of modules: examples, PIDs (24).
 260128-161104
260128-161104: The structure theorem of modules: examples, PIDs (23).
 260128-161103
260128-161103: The structure theorem of modules: examples, PIDs (22).
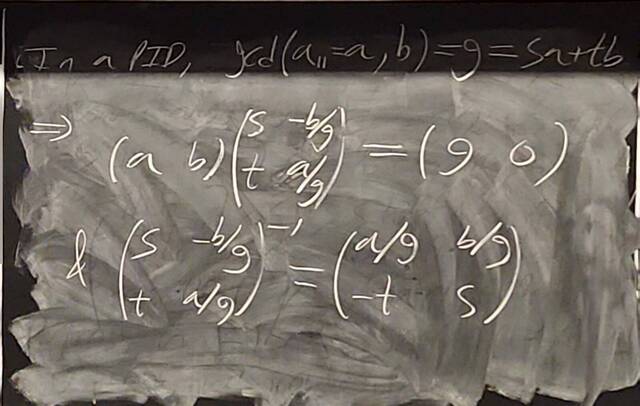 260128-161102
260128-161102: The structure theorem of modules: examples, PIDs (21).
 260128-161101
260128-161101: The structure theorem of modules: examples, PIDs (20).
 260128-161100
260128-161100: The structure theorem of modules: examples, PIDs (19).
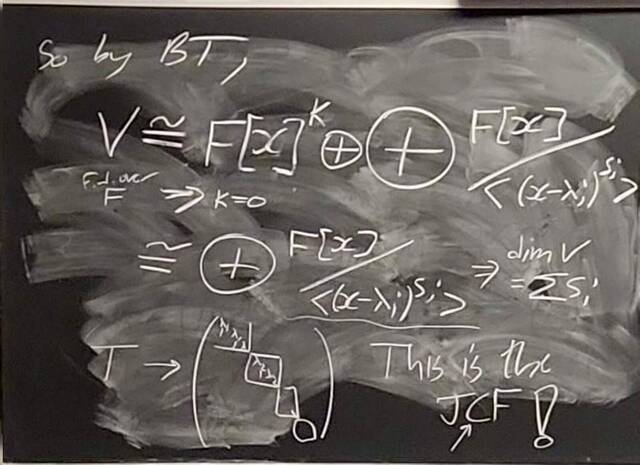 260128-161059
260128-161059: The structure theorem of modules: examples, PIDs (18).
 260128-161058
260128-161058: The structure theorem of modules: examples, PIDs (17).
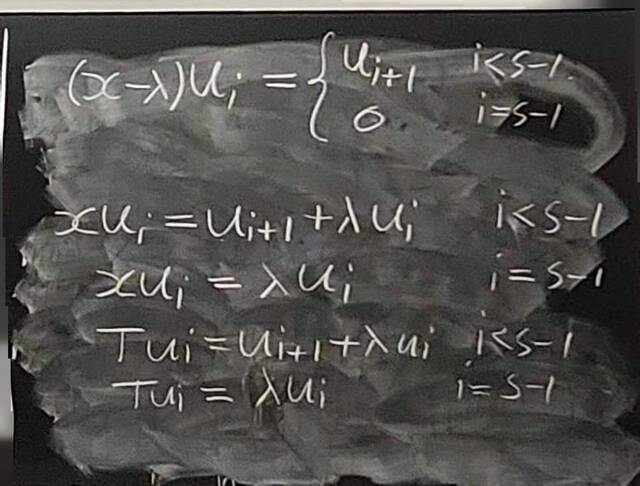 260128-161057
260128-161057: The structure theorem of modules: examples, PIDs (16).
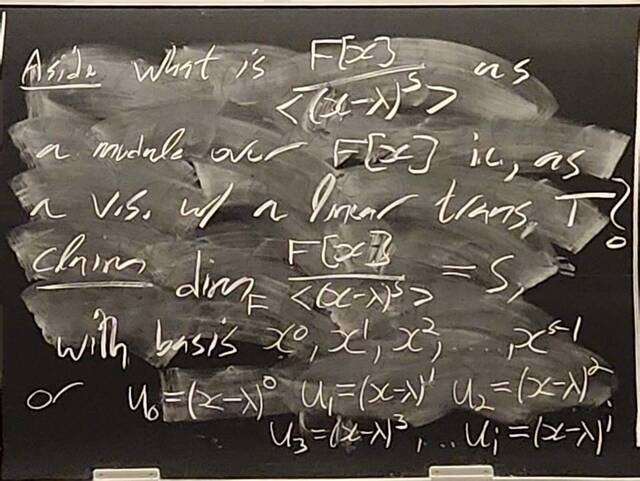 260128-161056
260128-161056: The structure theorem of modules: examples, PIDs (15).
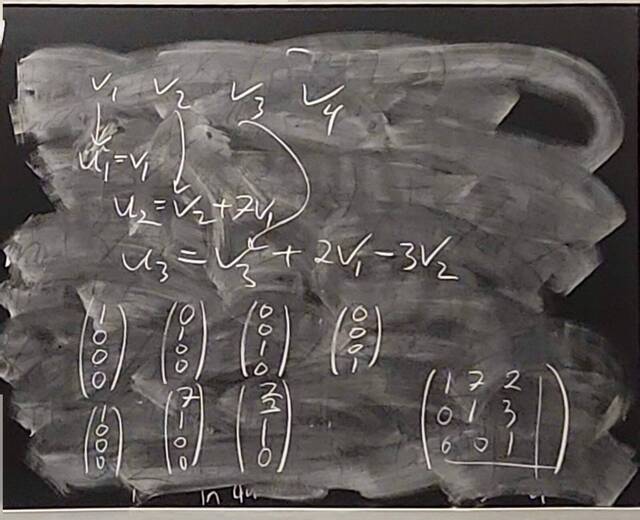 260128-161055
260128-161055: The structure theorem of modules: examples, PIDs (14).
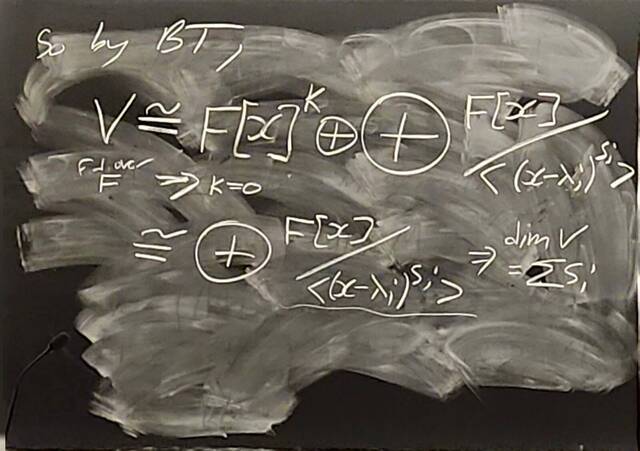 260128-161054
260128-161054: The structure theorem of modules: examples, PIDs (13).
 260128-161053
260128-161053: The structure theorem of modules: examples, PIDs (12).
 260128-161052
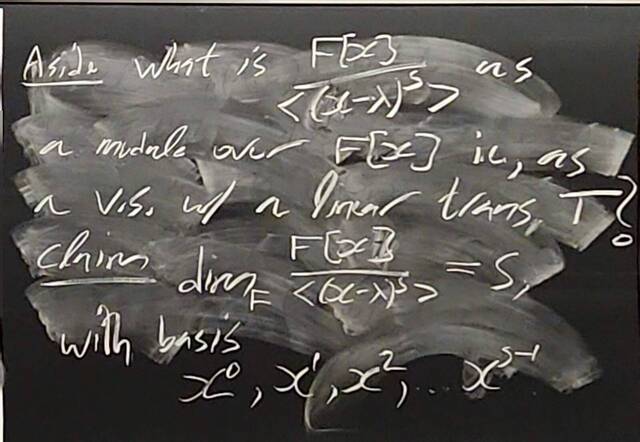
260128-161052: The structure theorem of modules: examples, PIDs (11).
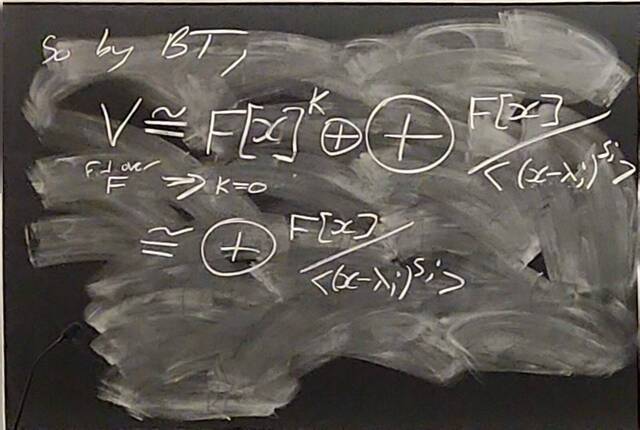 260128-161050
260128-161050: The structure theorem of modules: examples, PIDs (10).
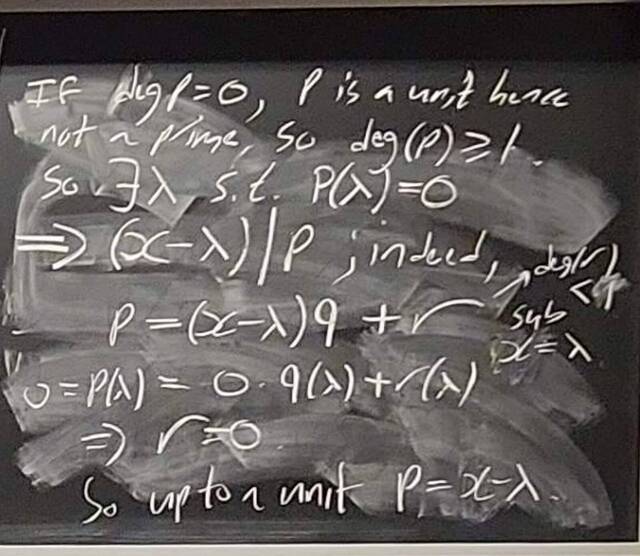 260128-161049
260128-161049: The structure theorem of modules: examples, PIDs (9).
 260128-161048
260128-161048: The structure theorem of modules: examples, PIDs (8).
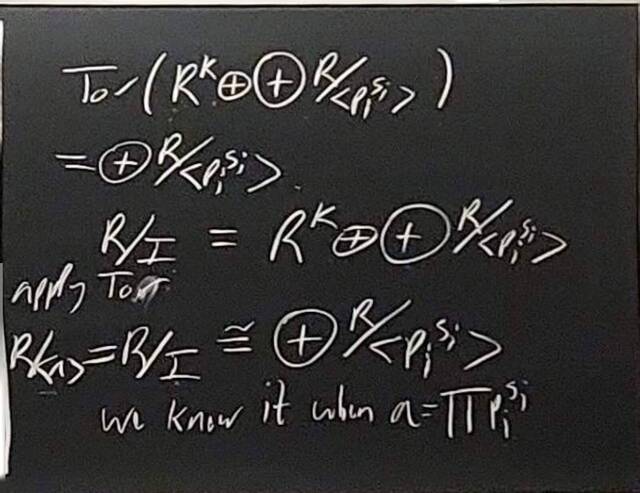 260128-161047
260128-161047: The structure theorem of modules: examples, PIDs (7).
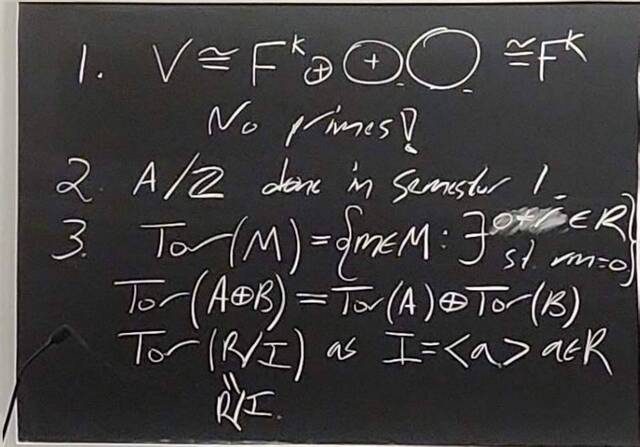 260128-161046
260128-161046: The structure theorem of modules: examples, PIDs (6).
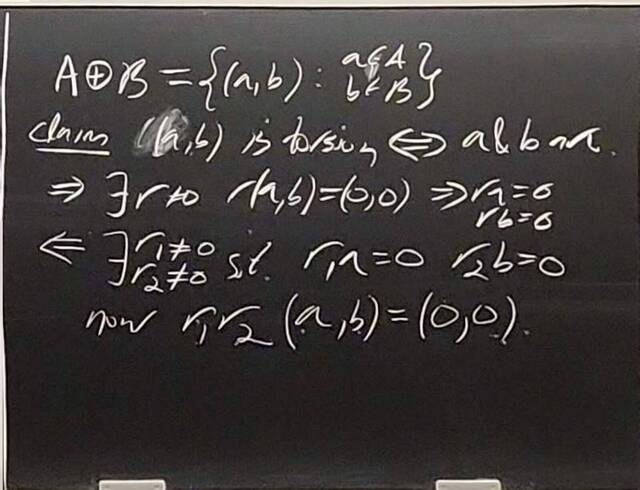 260128-161045
260128-161045: The structure theorem of modules: examples, PIDs (5).
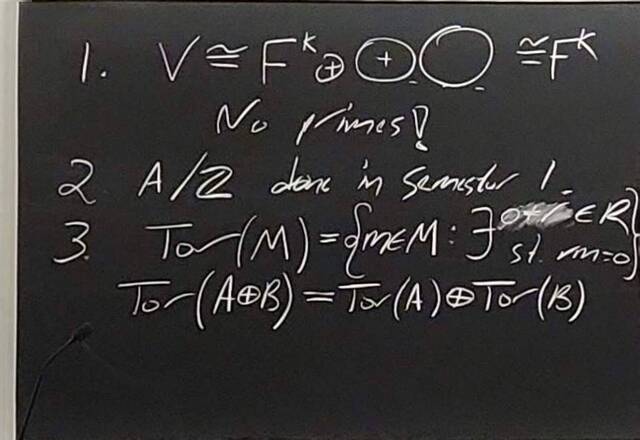 260128-161044
260128-161044: The structure theorem of modules: examples, PIDs (4).
 260128-161043
260128-161043: The structure theorem of modules: examples, PIDs (3).
 260128-161042
260128-161042: The structure theorem of modules: examples, PIDs (2).
 260107-123558
260107-123558: Jan 7 H37-38: Rings with similar properties to Z (7).
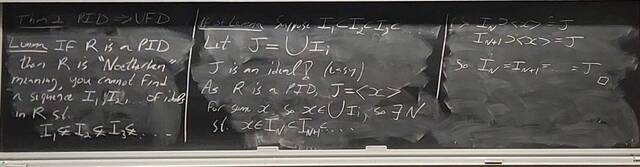 260107-123557
260107-123557: Jan 7 H37-38: Rings with similar properties to Z (6).
 260107-123556
260107-123556: Jan 7 H37-38: Rings with similar properties to Z (5).
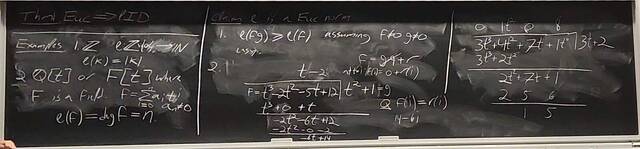 260107-123555
260107-123555: Jan 7 H37-38: Rings with similar properties to Z (4).
 260107-123554
260107-123554: Jan 7 H37-38: Rings with similar properties to Z (3).
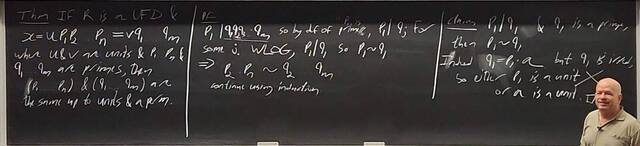 260107-123553
260107-123553: Jan 7 H37-38: Rings with similar properties to Z (2).
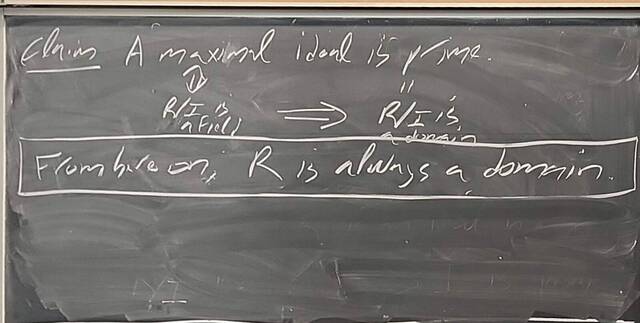 251126-130900
251126-130900: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (13).
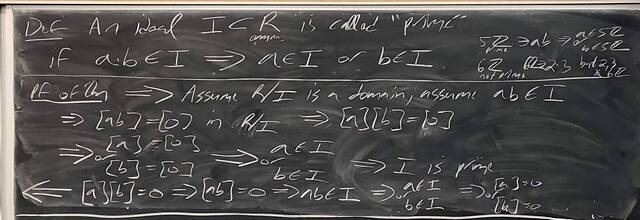 251126-130859
251126-130859: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (12).
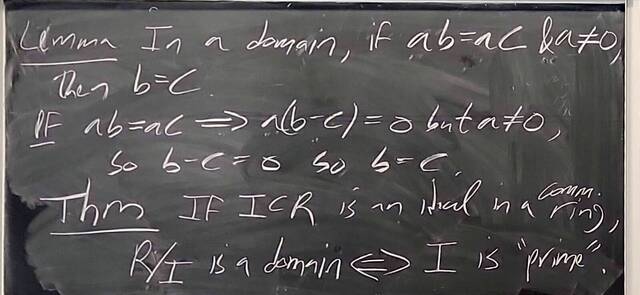 251126-130858
251126-130858: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (11).
 251126-130857
251126-130857: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (10).
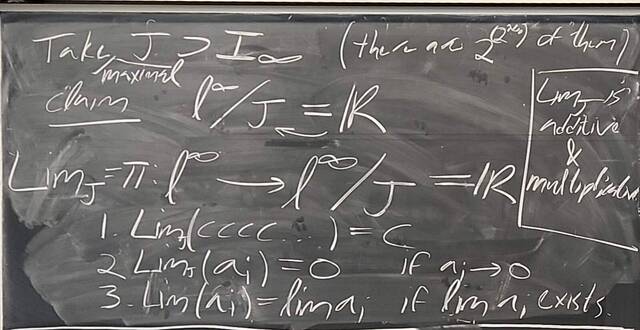 251126-130856
251126-130856: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (9).
 251126-130855
251126-130855: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (8).
 251126-130854
251126-130854: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (7).
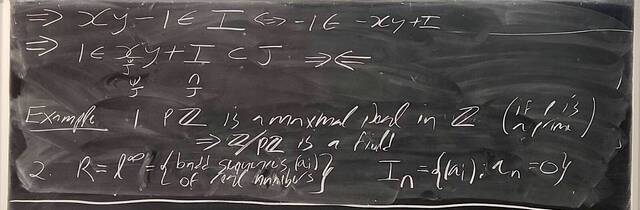 251126-130853
251126-130853: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (6).
 251126-130852
251126-130852: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (5).
 251126-130851
251126-130851: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (4).
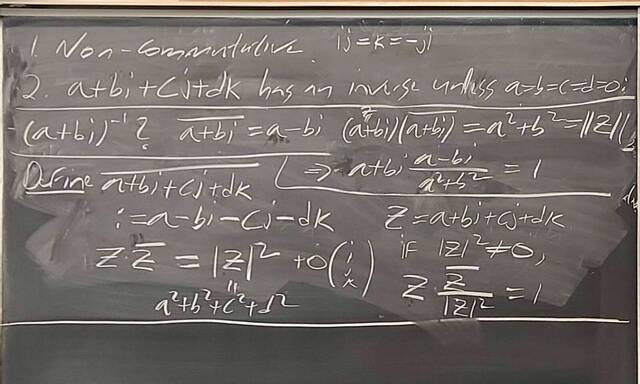 251126-130850
251126-130850: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (3).
 251126-130849
251126-130849: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals (2).
 251126-130848
251126-130848: Nov 26 H34-35: Fields and maximal ideals, domains and prime ideals.
 251119-170142
251119-170142: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (12).
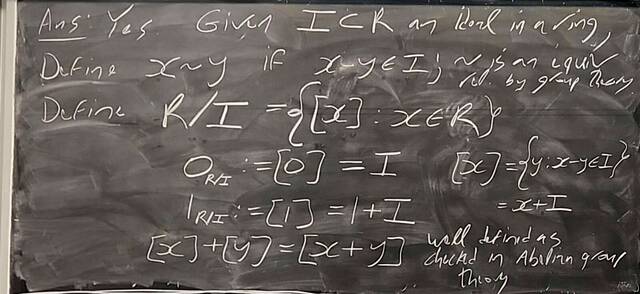 251119-170141
251119-170141: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (11).
 251119-170140
251119-170140: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (10).
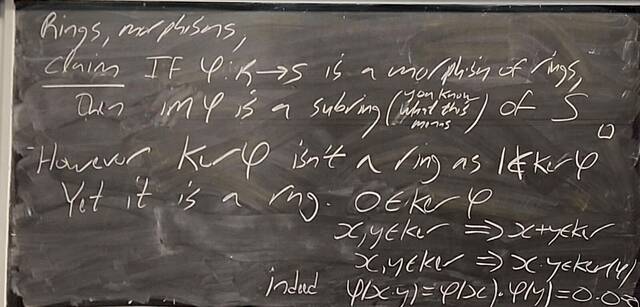 251119-170139
251119-170139: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (9).
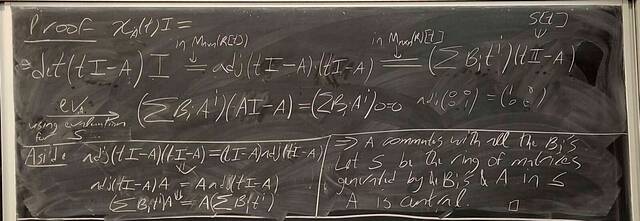 251119-170138
251119-170138: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (8).
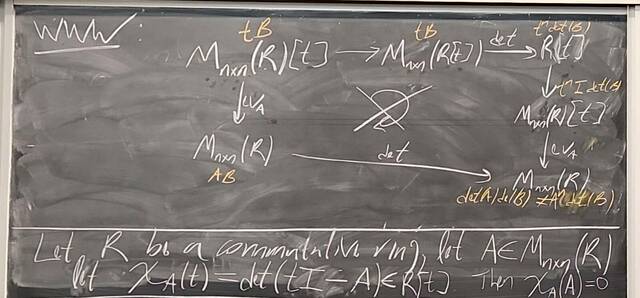 251119-170137
251119-170137: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (7).
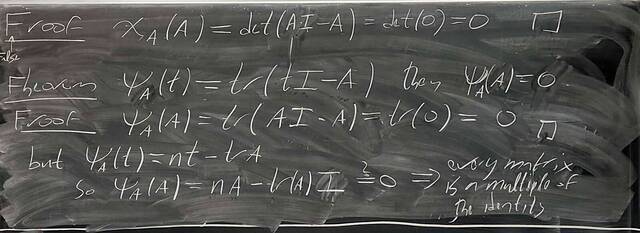 251119-170136
251119-170136: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (6).
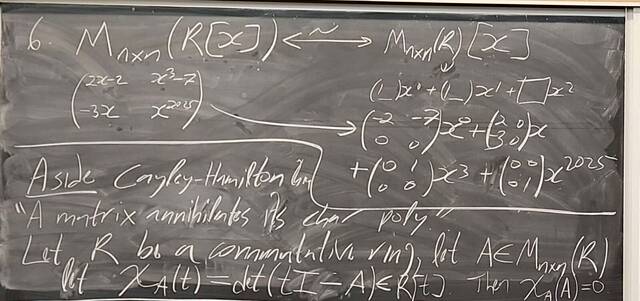 251119-170135
251119-170135: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (5).
 251119-170134
251119-170134: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (4).
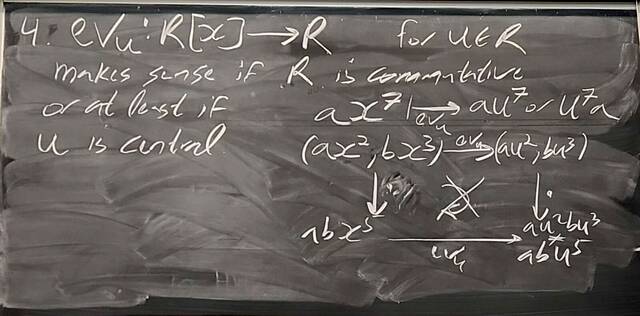 251119-170133
251119-170133: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (3).
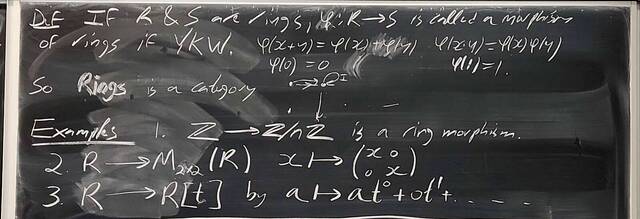 251119-170132
251119-170132: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients (2).
 251119-170131
251119-170131: Nov 19 H31-32: Morphisms of rings, Cayley-Hamilton, ideals, quotients.
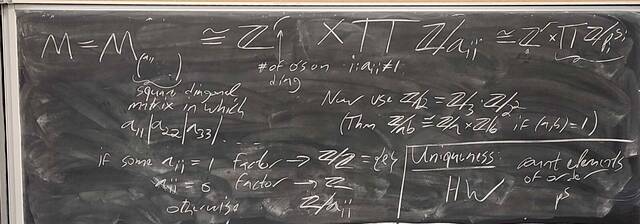 251112-125621
251112-125621: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (11).
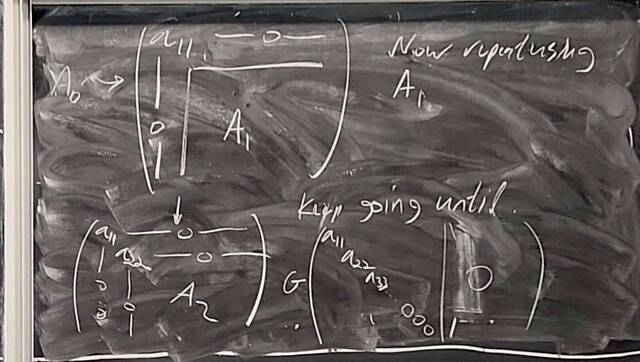 251112-125620
251112-125620: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (10).
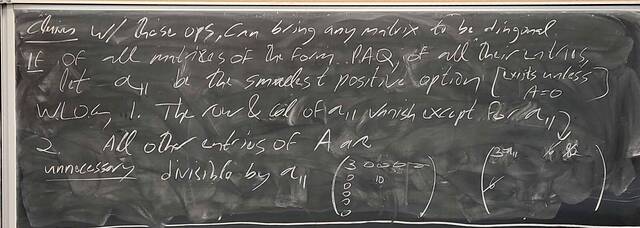 251112-125619
251112-125619: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (9).
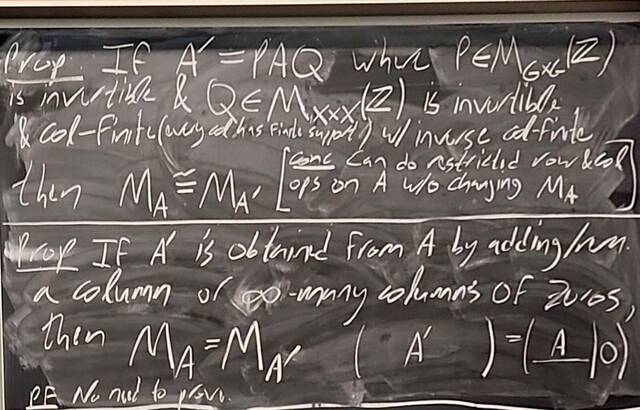 251112-125618
251112-125618: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (8).
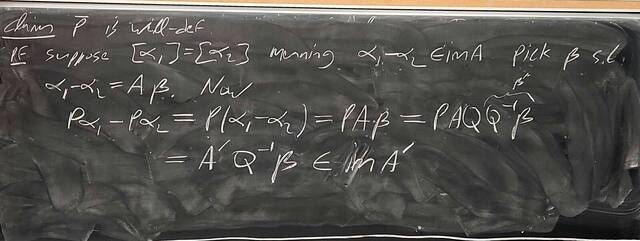 251112-125617
251112-125617: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (7).
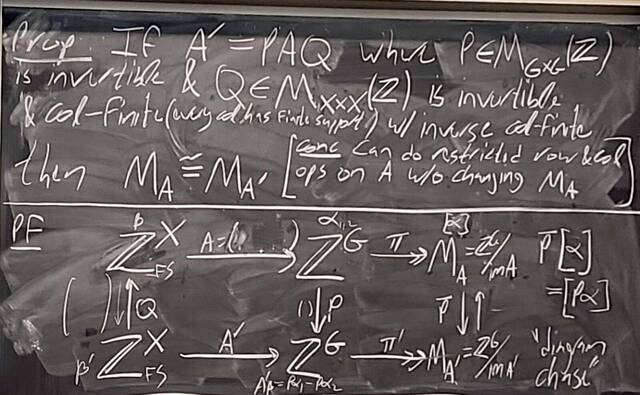 251112-125616
251112-125616: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (6).
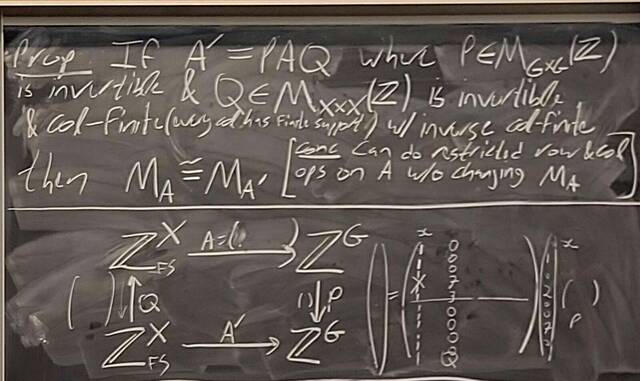 251112-125615
251112-125615: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (5).
 251112-125614
251112-125614: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (4).
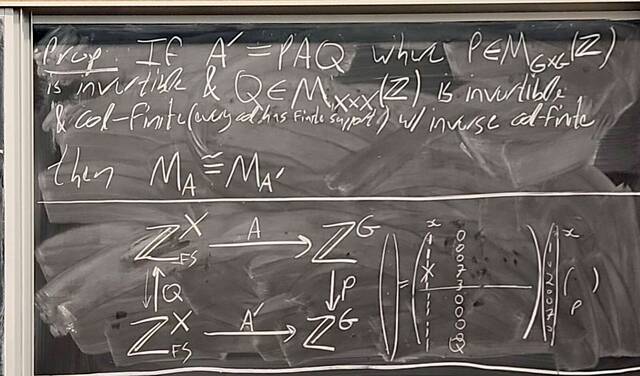 251112-125613
251112-125613: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (3).
 251112-125612
251112-125612: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups (2).
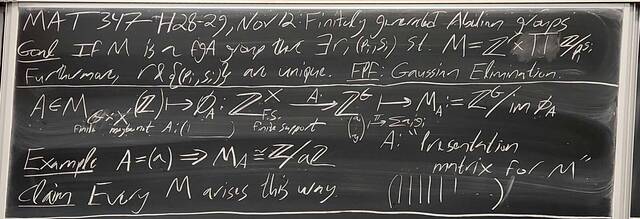 251112-125611
251112-125611: Nov 12 H28-29: Proof of the structure theorem for finitely generated Abelian groups.
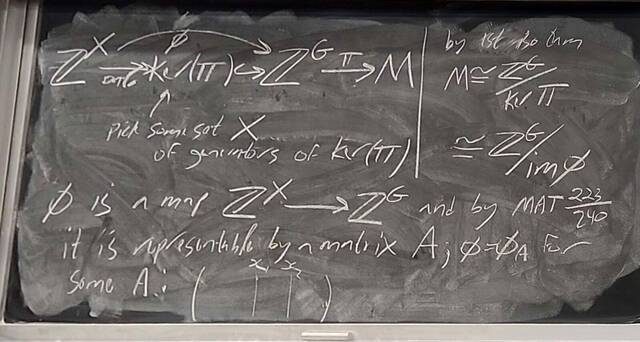 251107-162926
251107-162926: Nov 7 H27: FG Abelian groups and integer matrices (7).
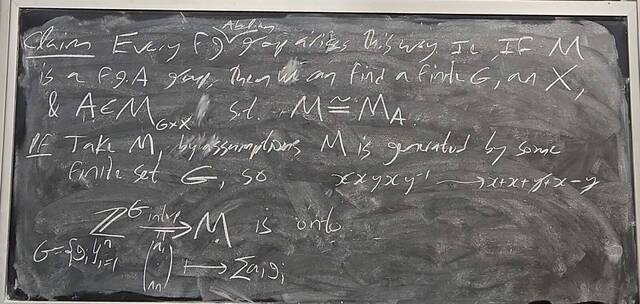 251107-162925
251107-162925: Nov 7 H27: FG Abelian groups and integer matrices (6).
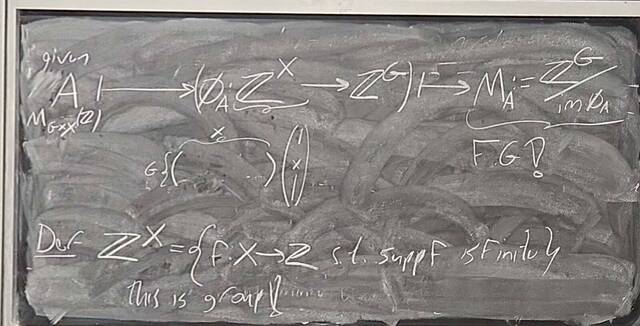 251107-162924
251107-162924: Nov 7 H27: FG Abelian groups and integer matrices (5).
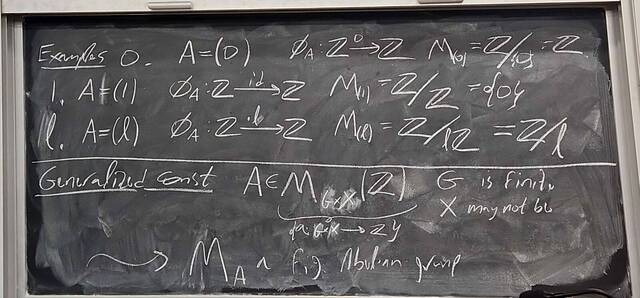 251107-162923
251107-162923: Nov 7 H27: FG Abelian groups and integer matrices (4).
 251107-162922
251107-162922: Nov 7 H27: FG Abelian groups and integer matrices (3).
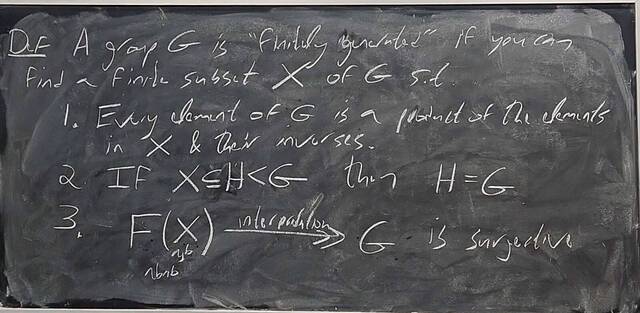 251107-162921
251107-162921: Nov 7 H27: FG Abelian groups and integer matrices (2).
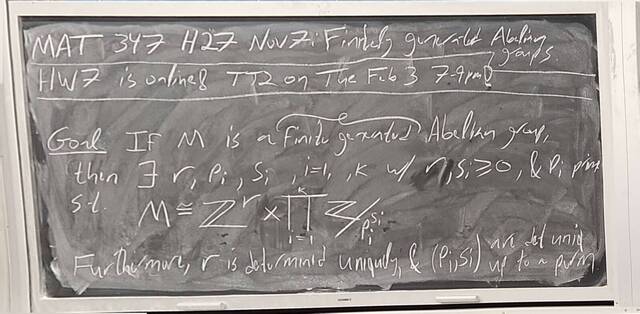 251107-162920
251107-162920: Nov 7 H27: FG Abelian groups and integer matrices.
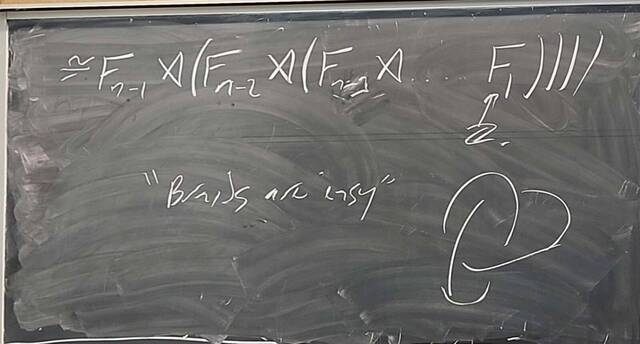 251105-133931
251105-133931: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (12).
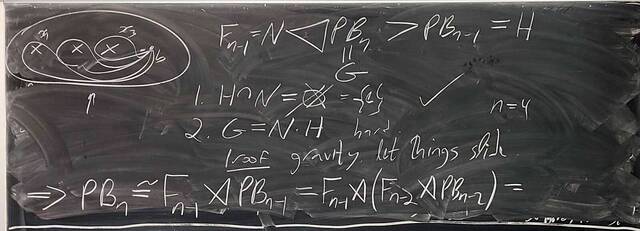 251105-133930
251105-133930: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (11).
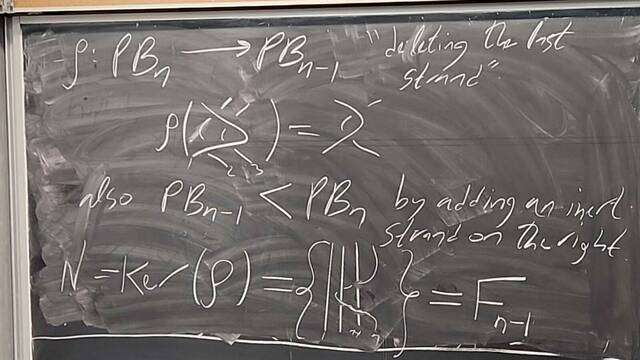 251105-133929
251105-133929: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (10).
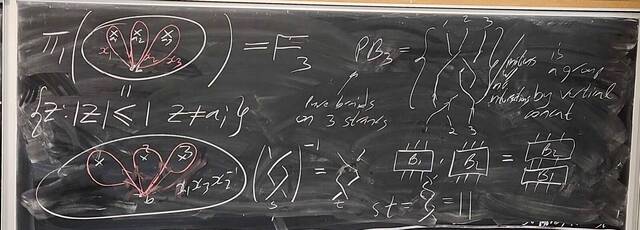 251105-133928
251105-133928: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (9).
 251105-133927
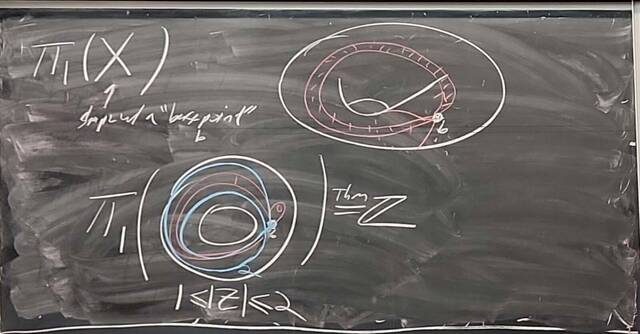
251105-133927: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (8).
 251105-133926
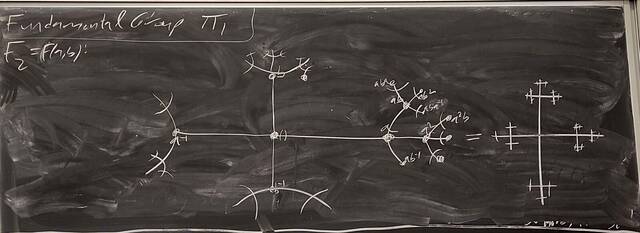
251105-133926: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (7).
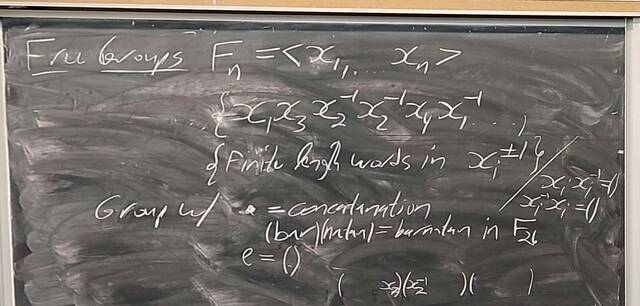 251105-133925
251105-133925: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (6).
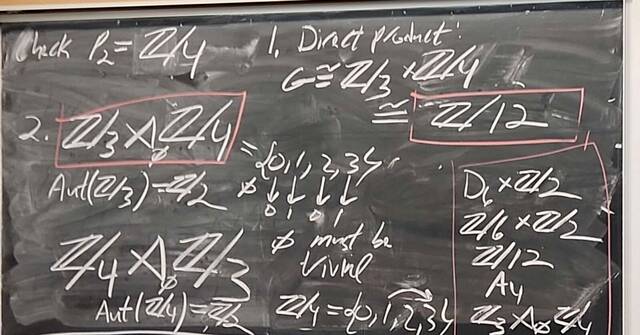 251105-133924
251105-133924: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (5).
 251105-133923
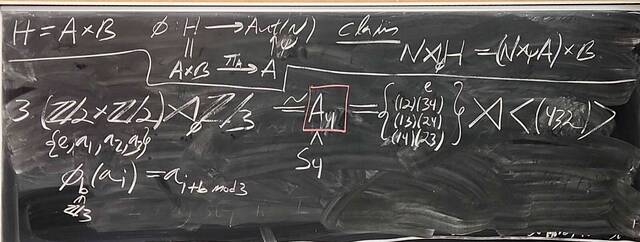
251105-133923: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (4).
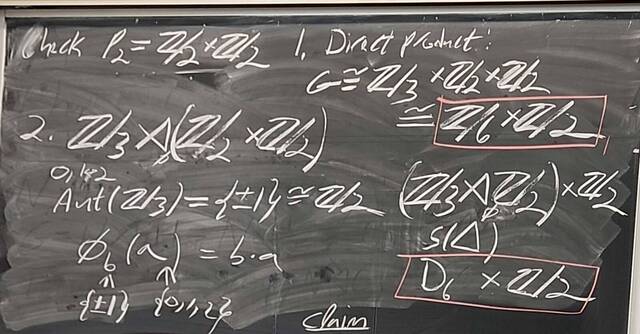 251105-133922
251105-133922: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (3).
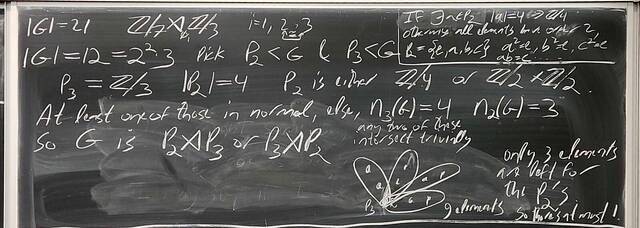 251105-133921
251105-133921: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids (2).
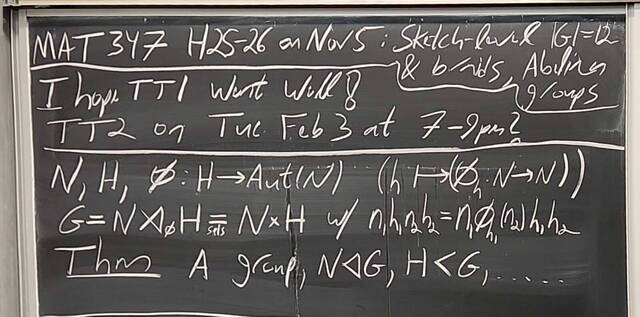 251105-133920
251105-133920: Nov 5 H25-26: $|G|=12$, free groups, $\pi_1$, and braids.
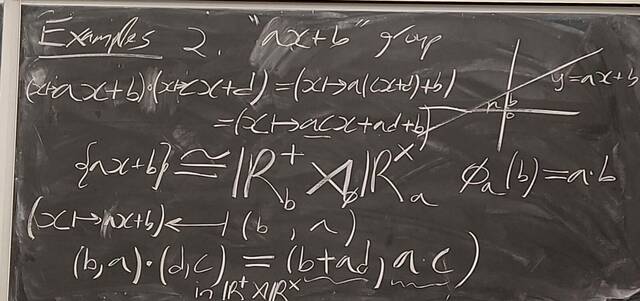 251023-062249
251023-062249: Oct 22 H22-23: Groups of order 21, semi-direct products (11).
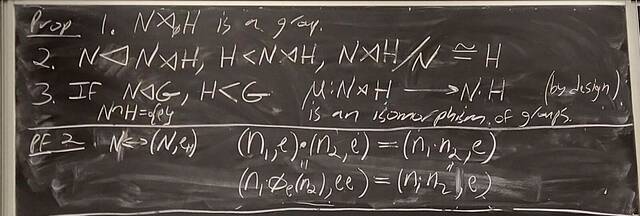 251023-062248
251023-062248: Oct 22 H22-23: Groups of order 21, semi-direct products (10).
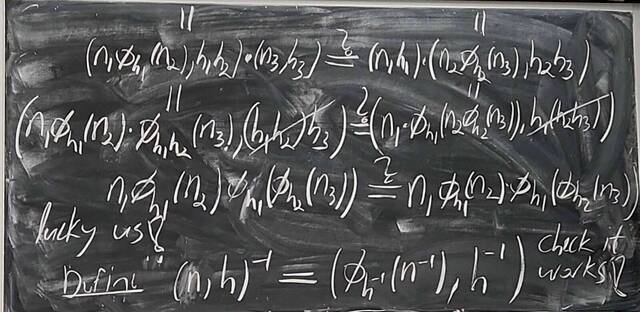 251023-062247
251023-062247: Oct 22 H22-23: Groups of order 21, semi-direct products (9).
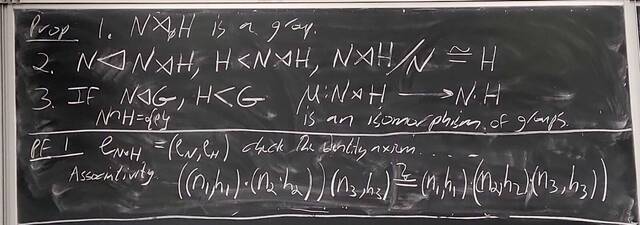 251023-062246
251023-062246: Oct 22 H22-23: Groups of order 21, semi-direct products (8).
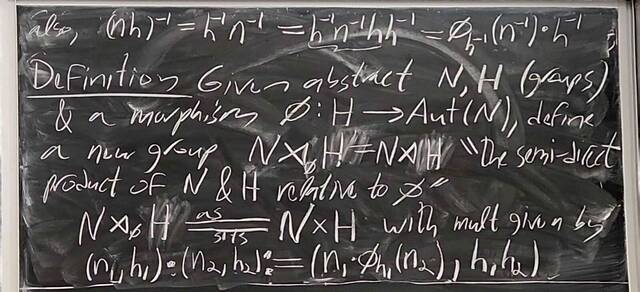 251023-062245
251023-062245: Oct 22 H22-23: Groups of order 21, semi-direct products (7).
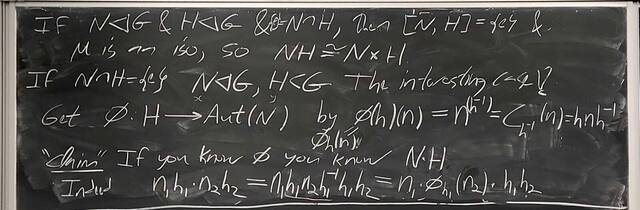 251023-062244
251023-062244: Oct 22 H22-23: Groups of order 21, semi-direct products (6).
 251023-062243
251023-062243: Oct 22 H22-23: Groups of order 21, semi-direct products (5).
 251023-062242
251023-062242: Oct 22 H22-23: Groups of order 21, semi-direct products (4).
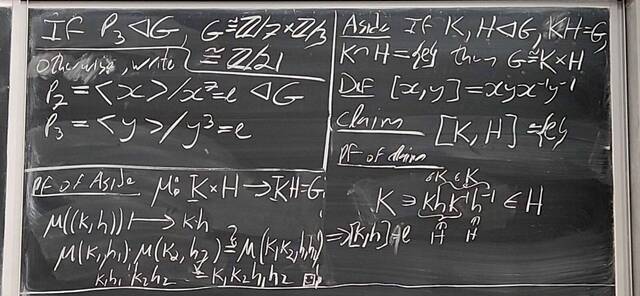 251023-062241
251023-062241: Oct 22 H22-23: Groups of order 21, semi-direct products (3).
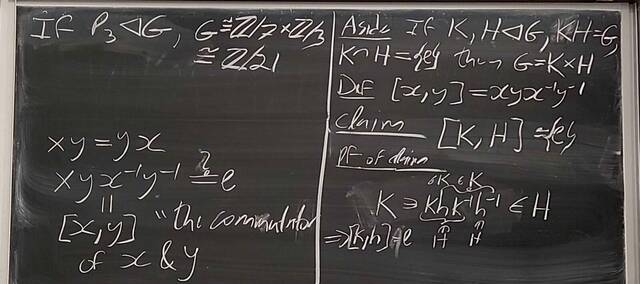 251023-062240
251023-062240: Oct 22 H22-23: Groups of order 21, semi-direct products (2).
 251023-062239
251023-062239: Oct 22 H22-23: Groups of order 21, semi-direct products.
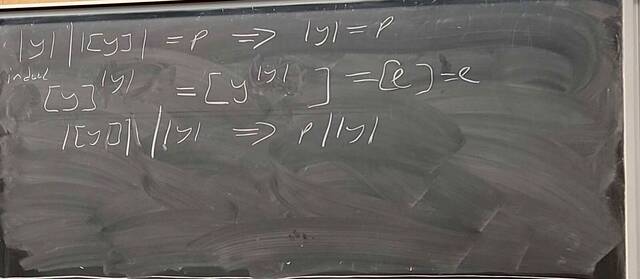 251015-124826
251015-124826: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (11).
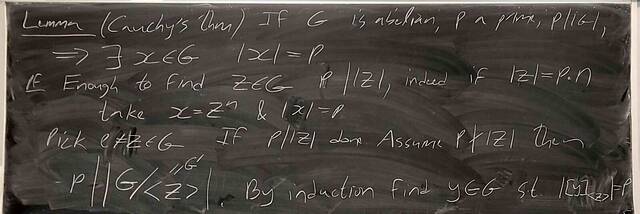 251015-124825
251015-124825: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (10).
 251015-124824
251015-124824: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (9).
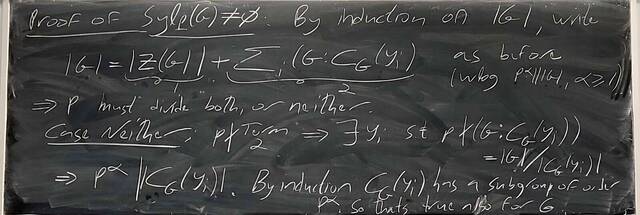 251015-124823
251015-124823: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (8).
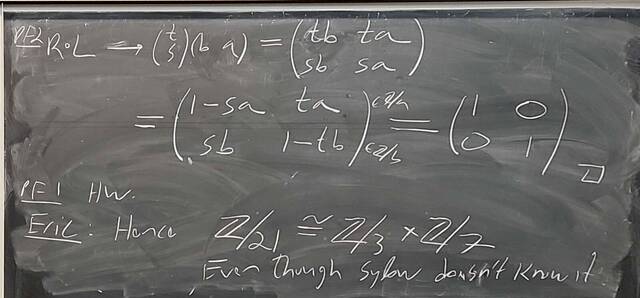 251015-124822
251015-124822: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (7).
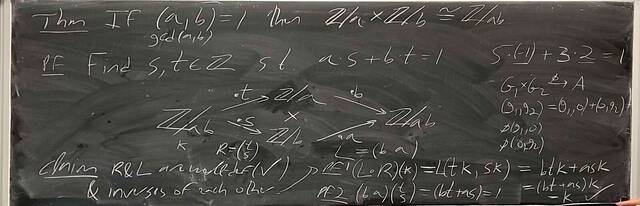 251015-124821
251015-124821: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (6).
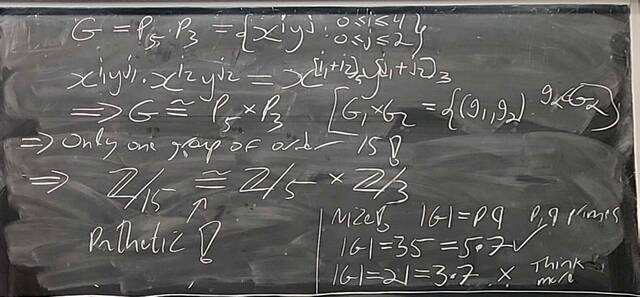 251015-124820
251015-124820: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (5).
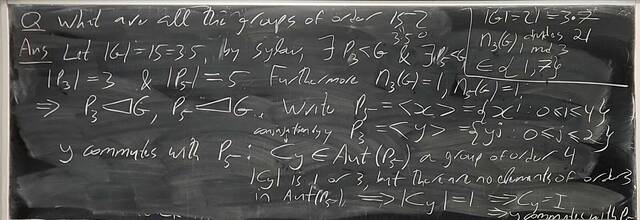 251015-124819
251015-124819: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (4).
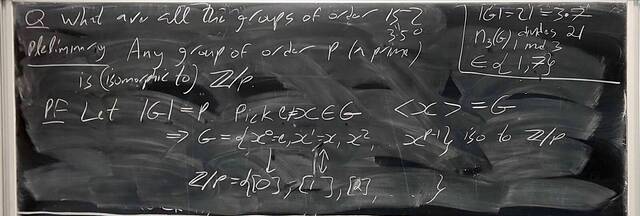 251015-124818
251015-124818: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (3).
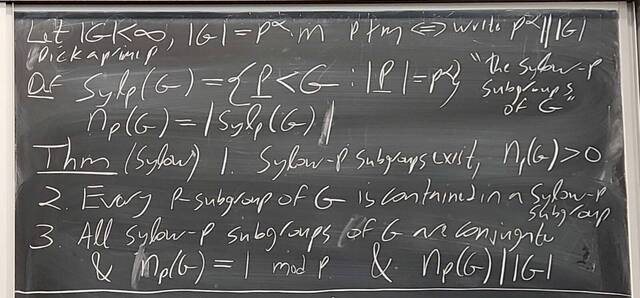 251015-124817
251015-124817: Oct 15 H19-20: The Sylow Theorem, groups of order 15 (2).
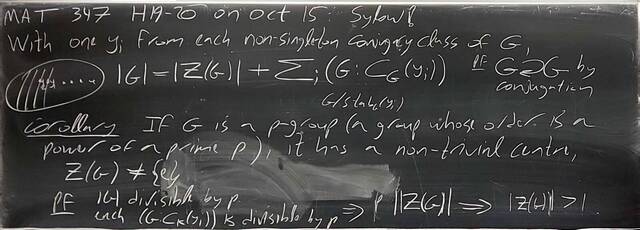 251015-124816
251015-124816: Oct 15 H19-20: The Sylow Theorem, groups of order 15.
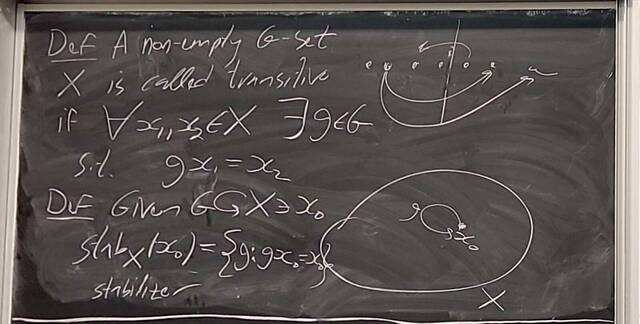 251008-130335
251008-130335: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (13).
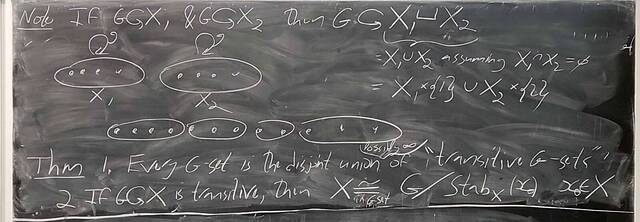 251008-130334
251008-130334: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (12).
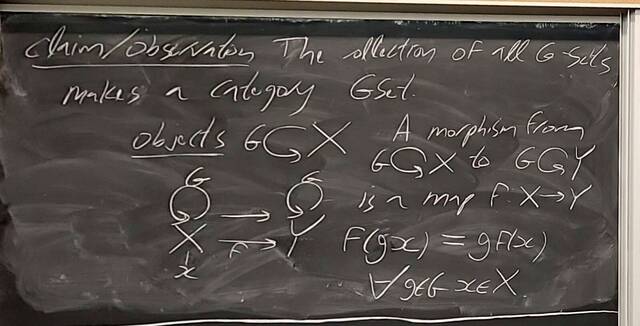 251008-130333
251008-130333: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (11).
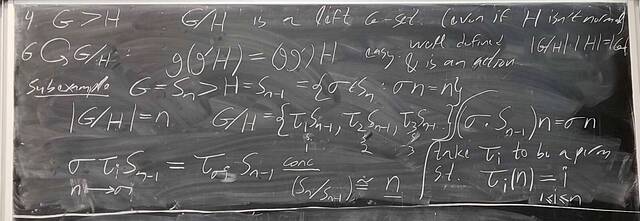 251008-130332
251008-130332: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (10).
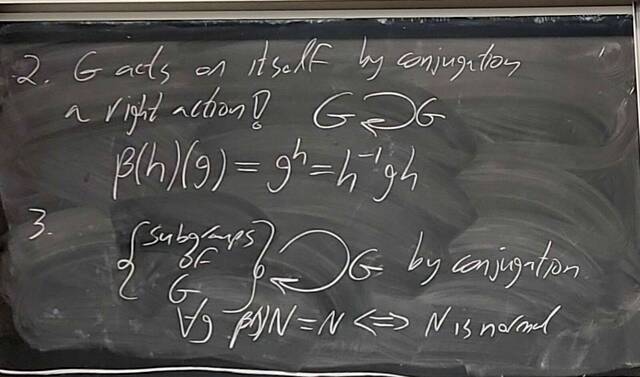 251008-130331
251008-130331: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (9).
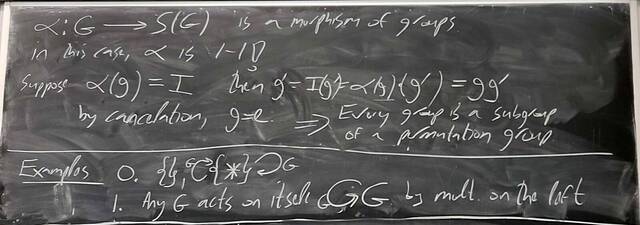 251008-130330
251008-130330: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (8).
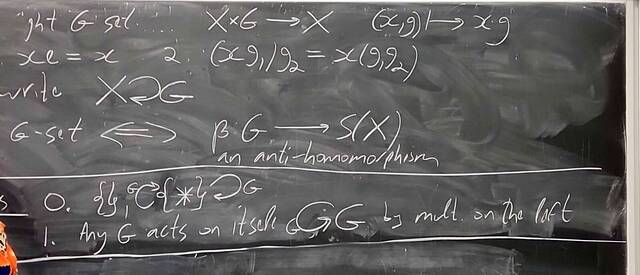 251008-130329
251008-130329: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (7).
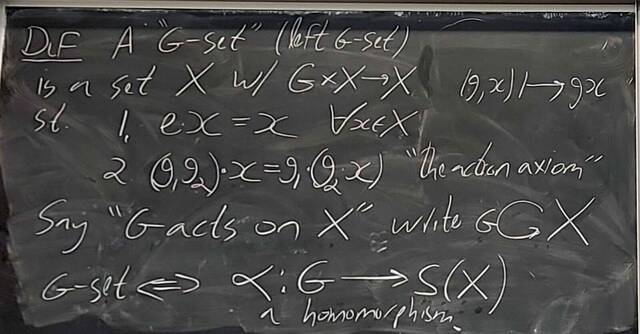 251008-130328
251008-130328: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (6).
 251008-130327
251008-130327: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (5).
 251008-130326
251008-130326: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (4).
 251008-130325
251008-130325: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (3).
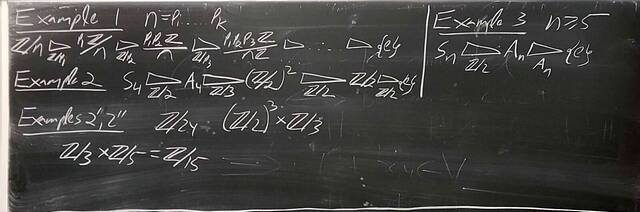 251008-130324
251008-130324: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions (2).
 251008-130323
251008-130323: Oct 8 Hours 16-17: Proof of Jordan-Holder, group actions.
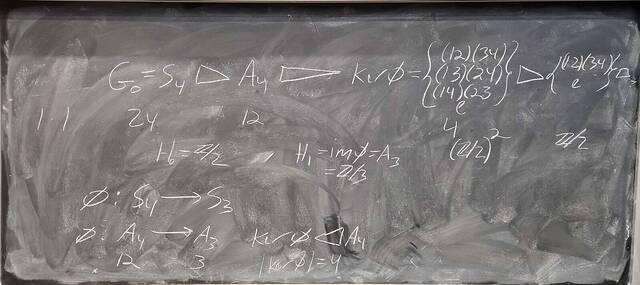 251003-150050
251003-150050: Oct 3 Hour 15: Simplicity of $A_n$, Jordan-Holder (6).
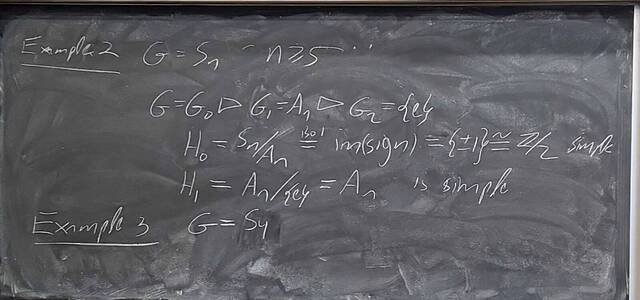 251003-150049
251003-150049: Oct 3 Hour 15: Simplicity of $A_n$, Jordan-Holder (5).
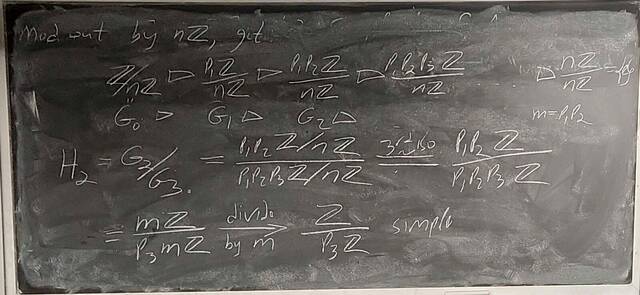 251003-150048
251003-150048: Oct 3 Hour 15: Simplicity of $A_n$, Jordan-Holder (4).
 251003-150047
251003-150047: Oct 3 Hour 15: Simplicity of $A_n$, Jordan-Holder (3).
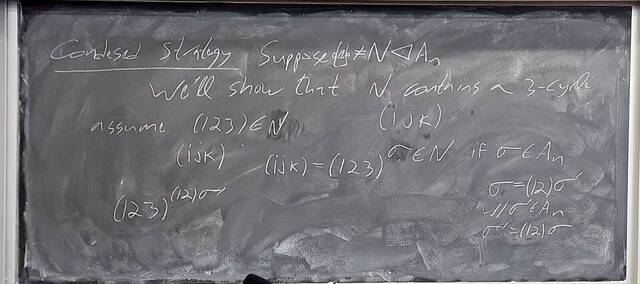 251003-150046
251003-150046: Oct 3 Hour 15: Simplicity of $A_n$, Jordan-Holder (2).
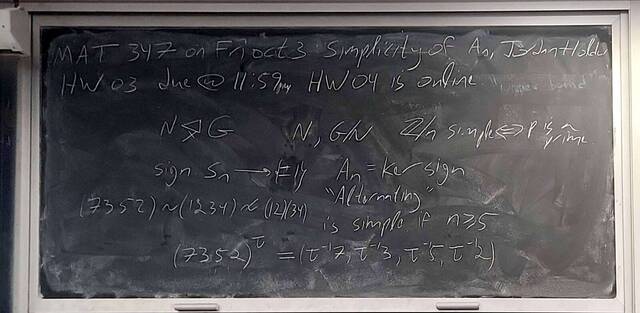 251003-150045
251003-150045: Oct 3 Hour 15: Simplicity of $A_n$, Jordan-Holder.
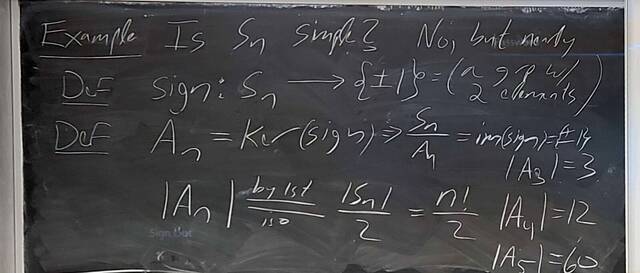 251001-123333
251001-123333: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$ (10).
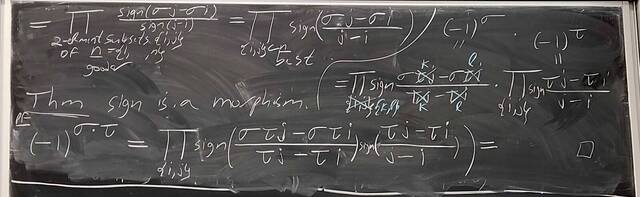 251001-123332
251001-123332: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$ (9).
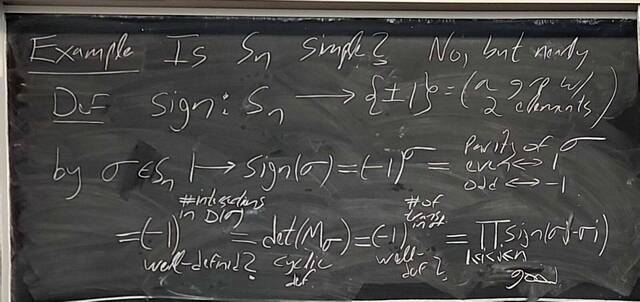 251001-123331
251001-123331: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$ (8).
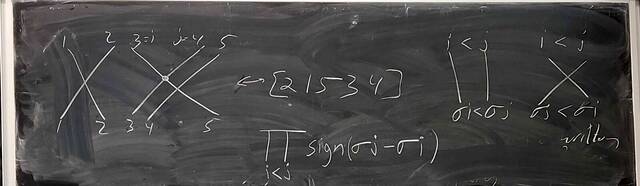 251001-123330
251001-123330: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$ (7).
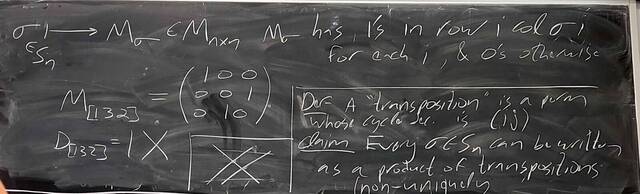 251001-123329
251001-123329: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$ (6).
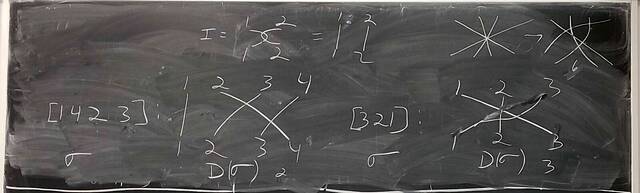 251001-123328
251001-123328: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$ (5).
 251001-123327
251001-123327: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$ (4).
 251001-123326
251001-123326: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$ (3).
 251001-123325
251001-123325: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$ (2).
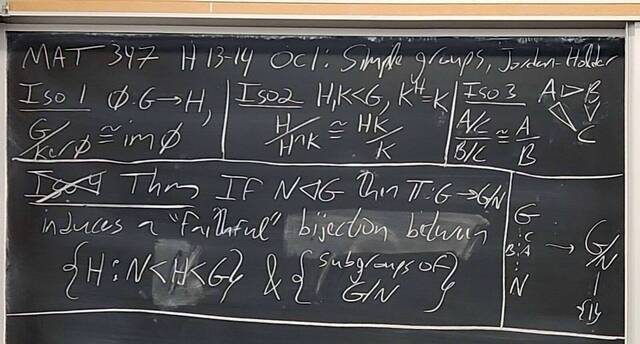 251001-123324
251001-123324: Oct 1 Hours 13-14: Simple groups, signs of permutations, the simplicity of $A_n$.
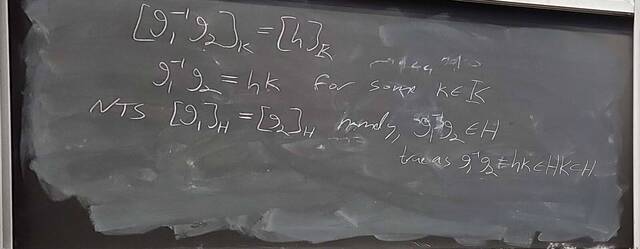 250926-130020
250926-130020: Sep 26 Hour 12: The 2nd and 3rd Isomorphism Theorem (6).
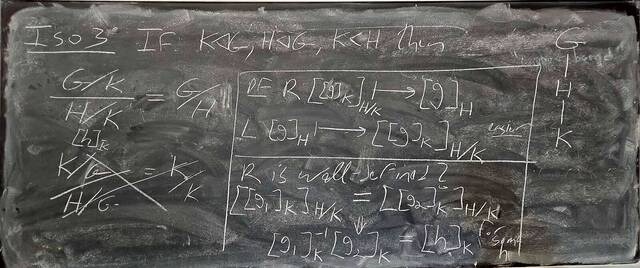 250926-130019
250926-130019: Sep 26 Hour 12: The 2nd and 3rd Isomorphism Theorem (5).
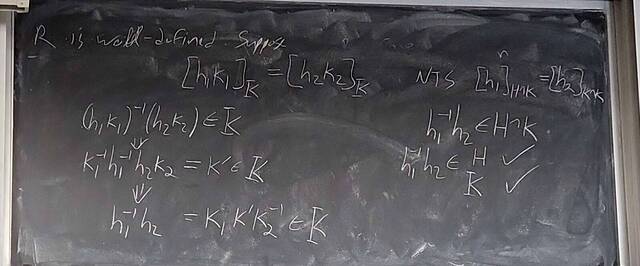 250926-130018
250926-130018: Sep 26 Hour 12: The 2nd and 3rd Isomorphism Theorem (4).
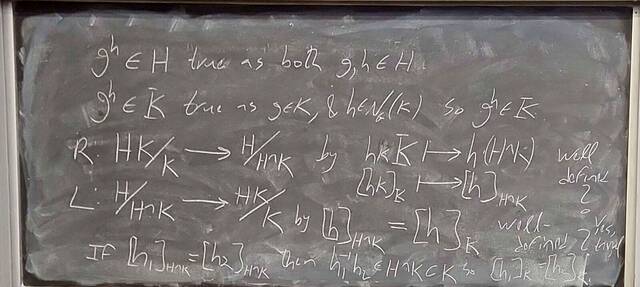 250926-130017
250926-130017: Sep 26 Hour 12: The 2nd and 3rd Isomorphism Theorem (3).
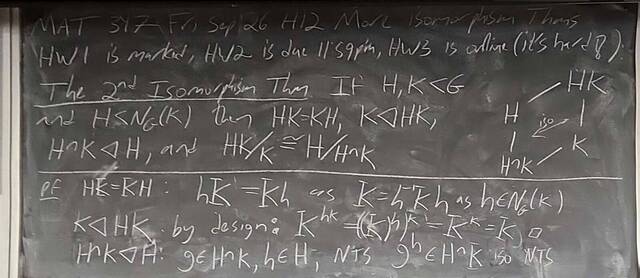 250926-130016
250926-130016: Sep 26 Hour 12: The 2nd and 3rd Isomorphism Theorem (2).
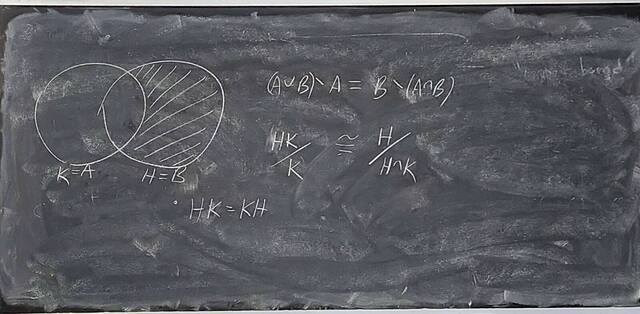 250926-130015
250926-130015: Sep 26 Hour 12: The 2nd and 3rd Isomorphism Theorem.
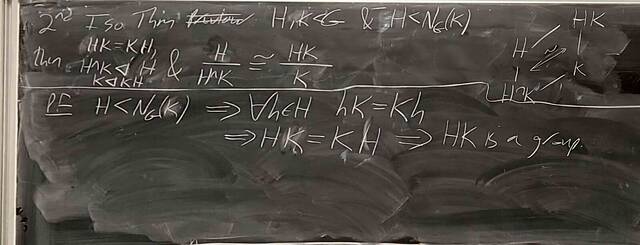 250924-124845
250924-124845: Sep 24 Hours 10-11: The isomorphism theorems (11).
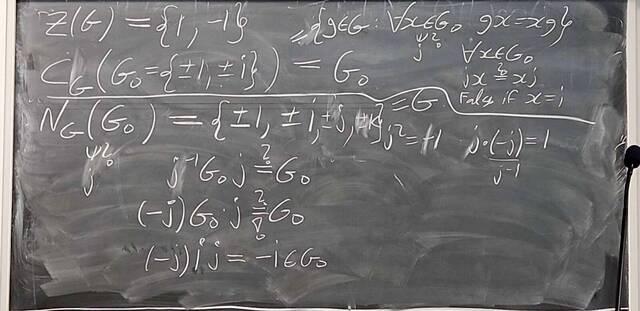 250924-124844
250924-124844: Sep 24 Hours 10-11: The isomorphism theorems (10).
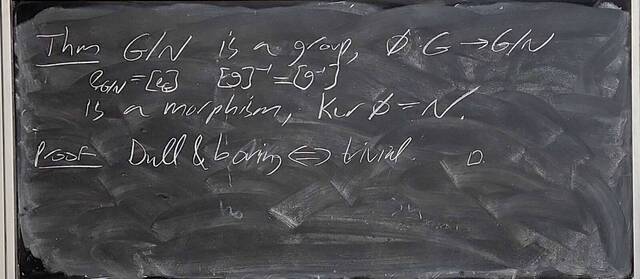 250919-131432
250919-131432: Sep 19 Hour 9: The quotient group construction (8).
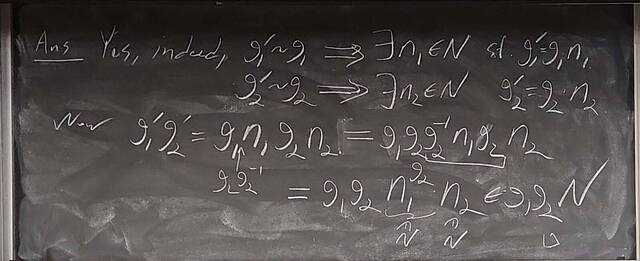 250919-131431
250919-131431: Sep 19 Hour 9: The quotient group construction (7).
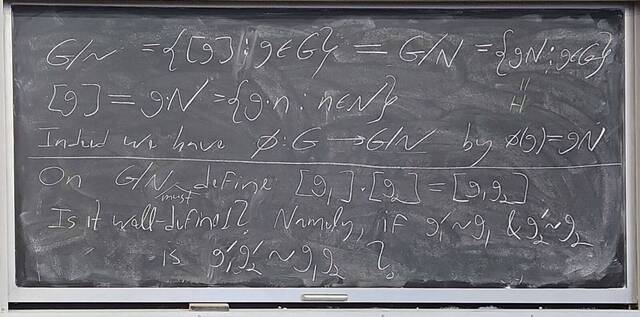 250919-131430
250919-131430: Sep 19 Hour 9: The quotient group construction (6).
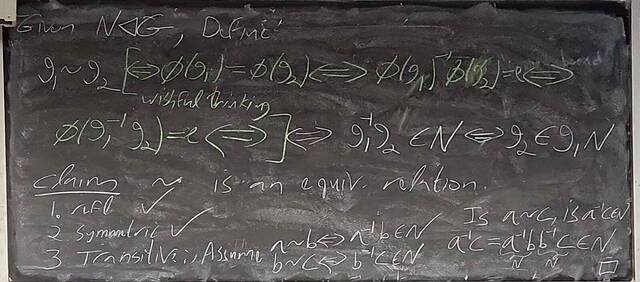 250919-131429
250919-131429: Sep 19 Hour 9: The quotient group construction (5).
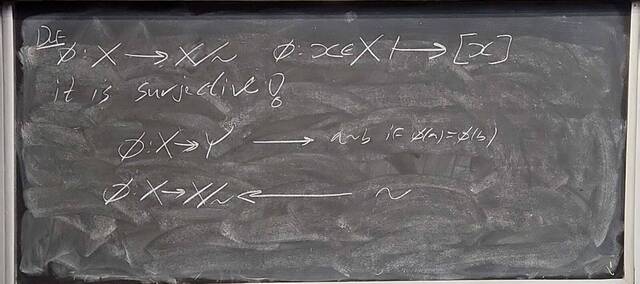 250919-131428
250919-131428: Sep 19 Hour 9: The quotient group construction (4).
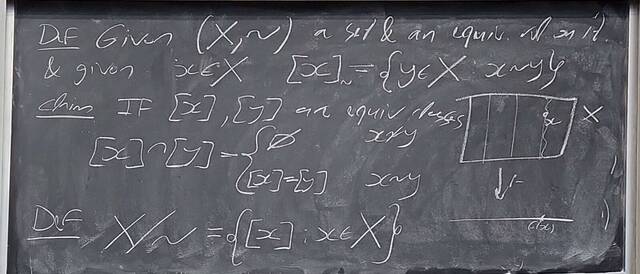 250919-131427
250919-131427: Sep 19 Hour 9: The quotient group construction (3).
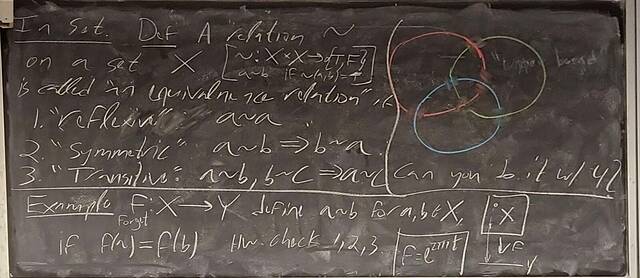 250919-131426
250919-131426: Sep 19 Hour 9: The quotient group construction (2).
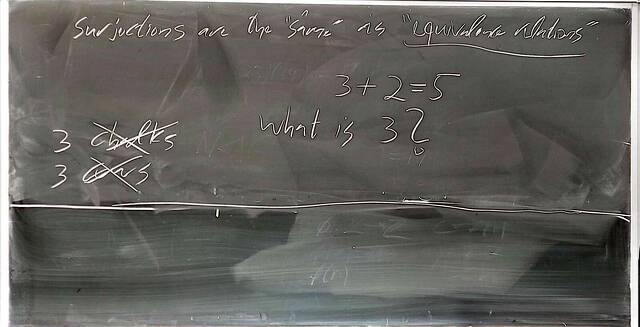 250917-122528
250917-122528: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (18).
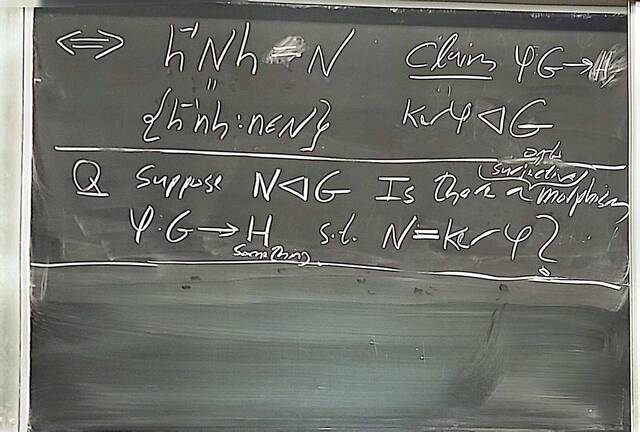 250917-122527
250917-122527: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (17).
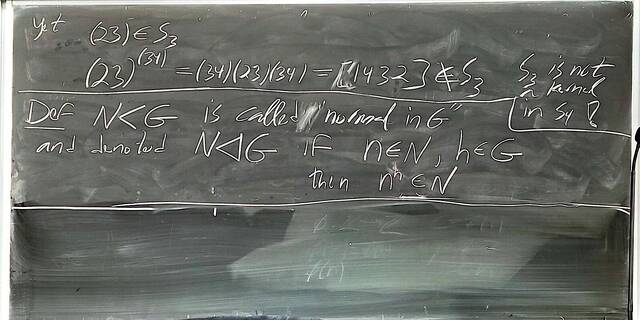 250917-122526
250917-122526: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (16).
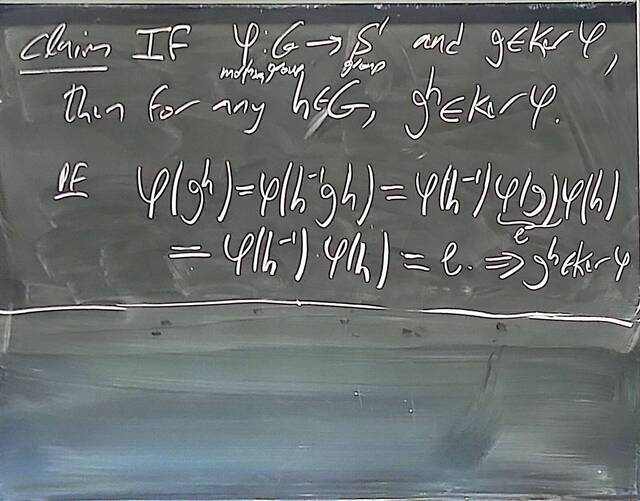 250917-122525
250917-122525: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (15).
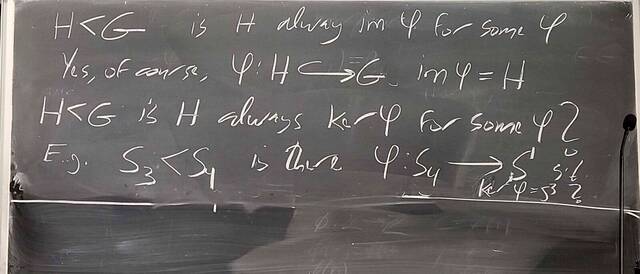 250917-122524
250917-122524: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (14).
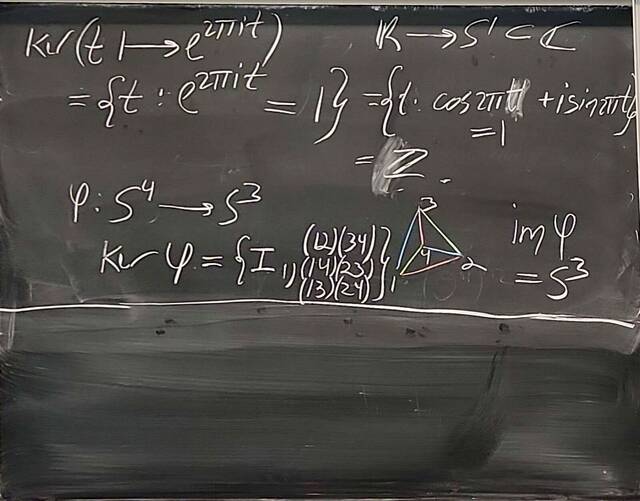 250917-122523
250917-122523: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (13).
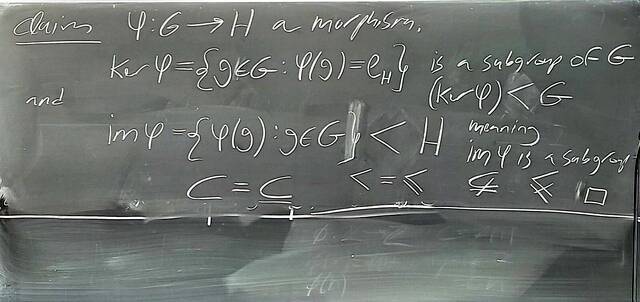 250917-122522
250917-122522: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (12).
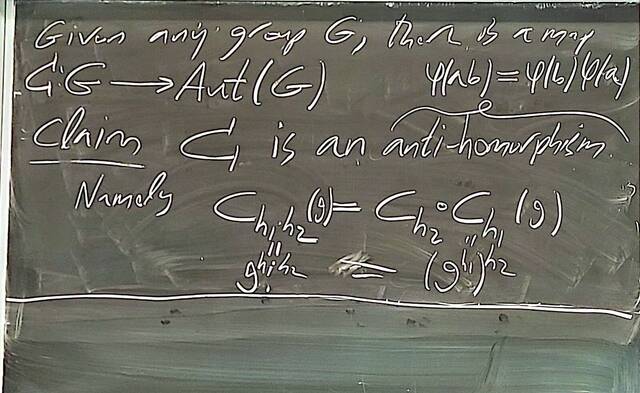 250917-122521
250917-122521: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (11).
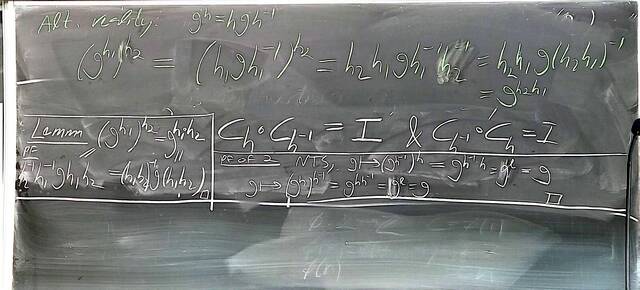 250917-122520
250917-122520: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (10).
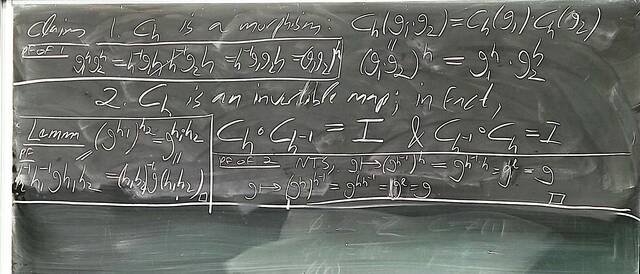 250917-122519
250917-122519: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (9).
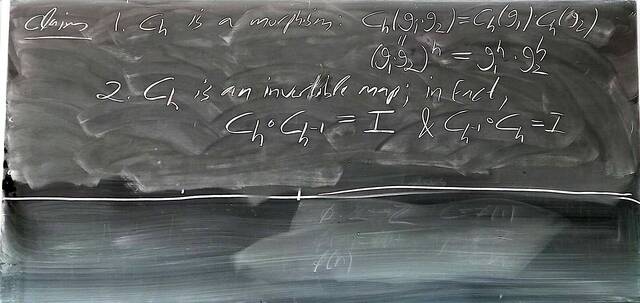 250917-122518
250917-122518: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (8).
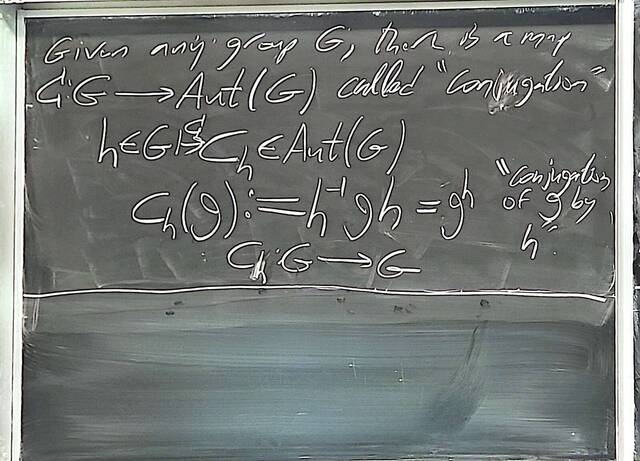 250917-122517
250917-122517: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (7).
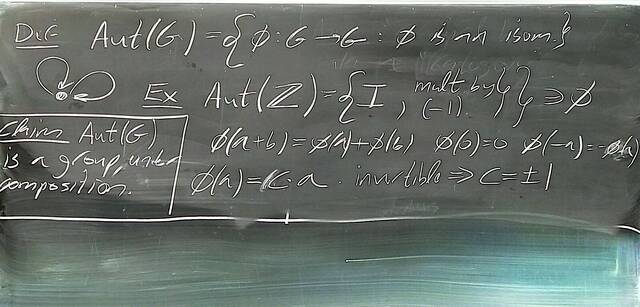 250917-122516
250917-122516: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (6).
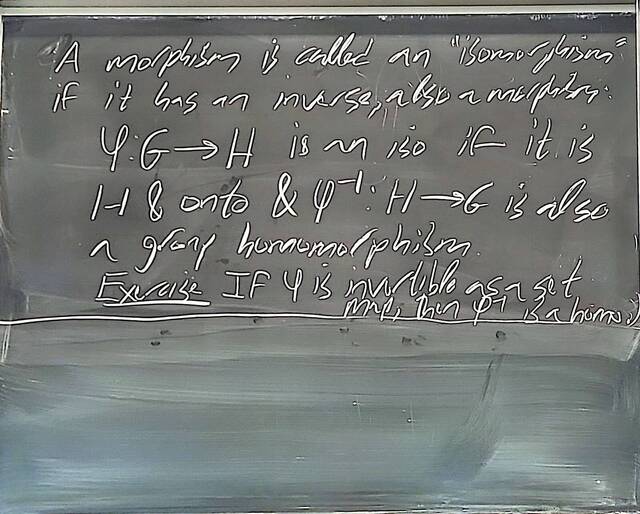 250917-122515
250917-122515: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (5).
 250917-122514
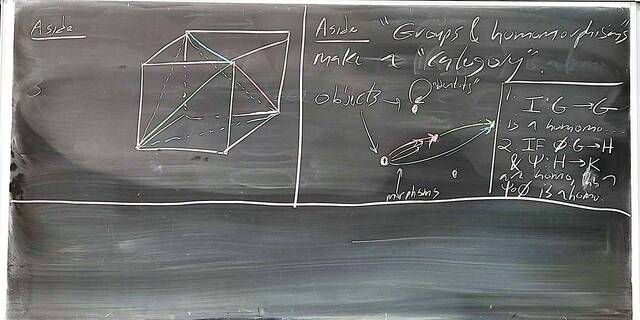
250917-122514: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (4).
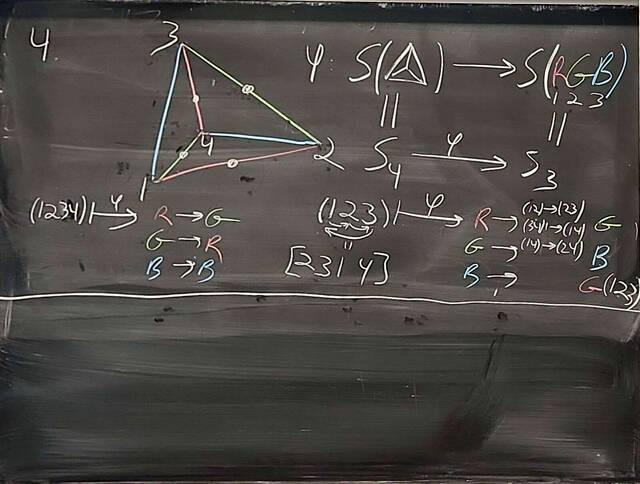 250917-122513
250917-122513: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (3).
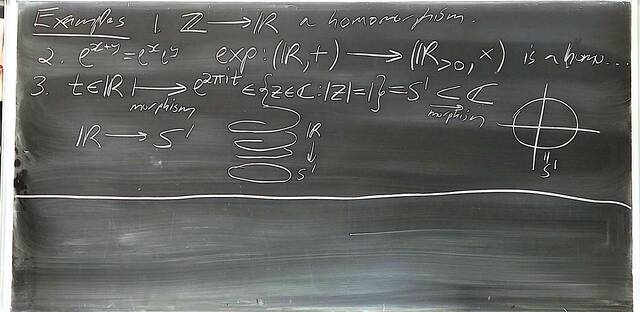 250917-122512
250917-122512: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups (2).
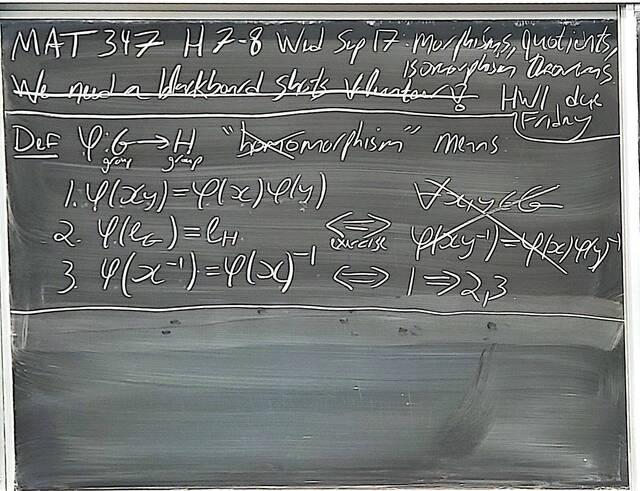 250917-122511
250917-122511: Sep 17 Hours 7-8: Homomorphisms, conjugations, kernels, images, normal subgroups.
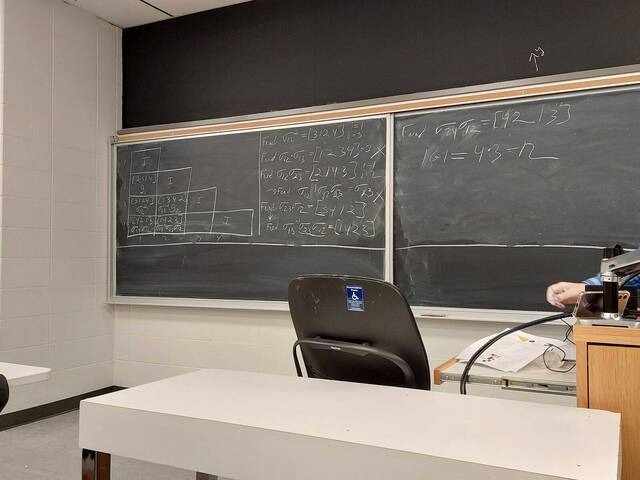 250910-115809
250910-115809: Sep 10 Hours 4-5: Even more Non-Commutative Gaussian Elimination (7).
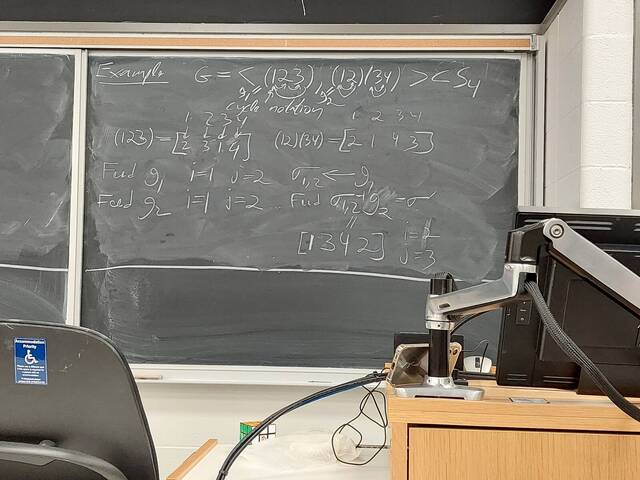 250910-114325
250910-114325: Sep 10 Hours 4-5: Even more Non-Commutative Gaussian Elimination (6).
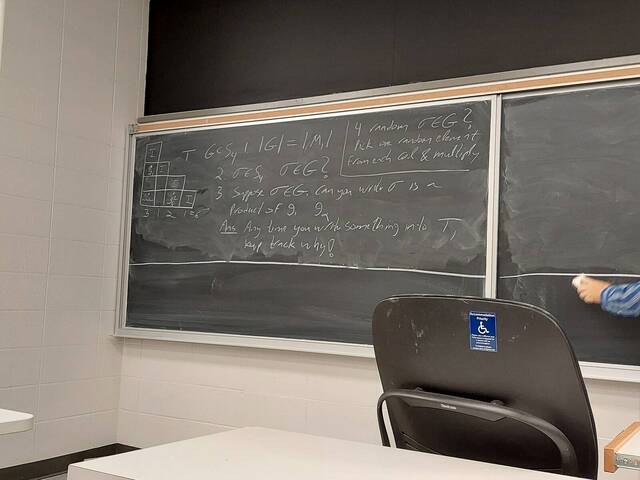 250910-113126
250910-113126: Sep 10 Hours 4-5: Even more Non-Commutative Gaussian Elimination (5).
 250910-112545
250910-112545: Sep 10 Hours 4-5: Even more Non-Commutative Gaussian Elimination (4).
 250910-105510
250910-105510: Sep 10 Hours 4-5: Even more Non-Commutative Gaussian Elimination (3).
 250910-105004
250910-105004: Sep 10 Hours 4-5: Even more Non-Commutative Gaussian Elimination (2).
 250910-104537
250910-104537: Sep 10 Hours 4-5: Even more Non-Commutative Gaussian Elimination.
 250905-122041
250905-122041: Sep 5 Hour 3: More Non-Commutative Gaussian Elimination (3).
 250905-122040
250905-122040: Sep 5 Hour 3: More Non-Commutative Gaussian Elimination (2).
 250905-122039
250905-122039: Sep 5 Hour 3: More Non-Commutative Gaussian Elimination.