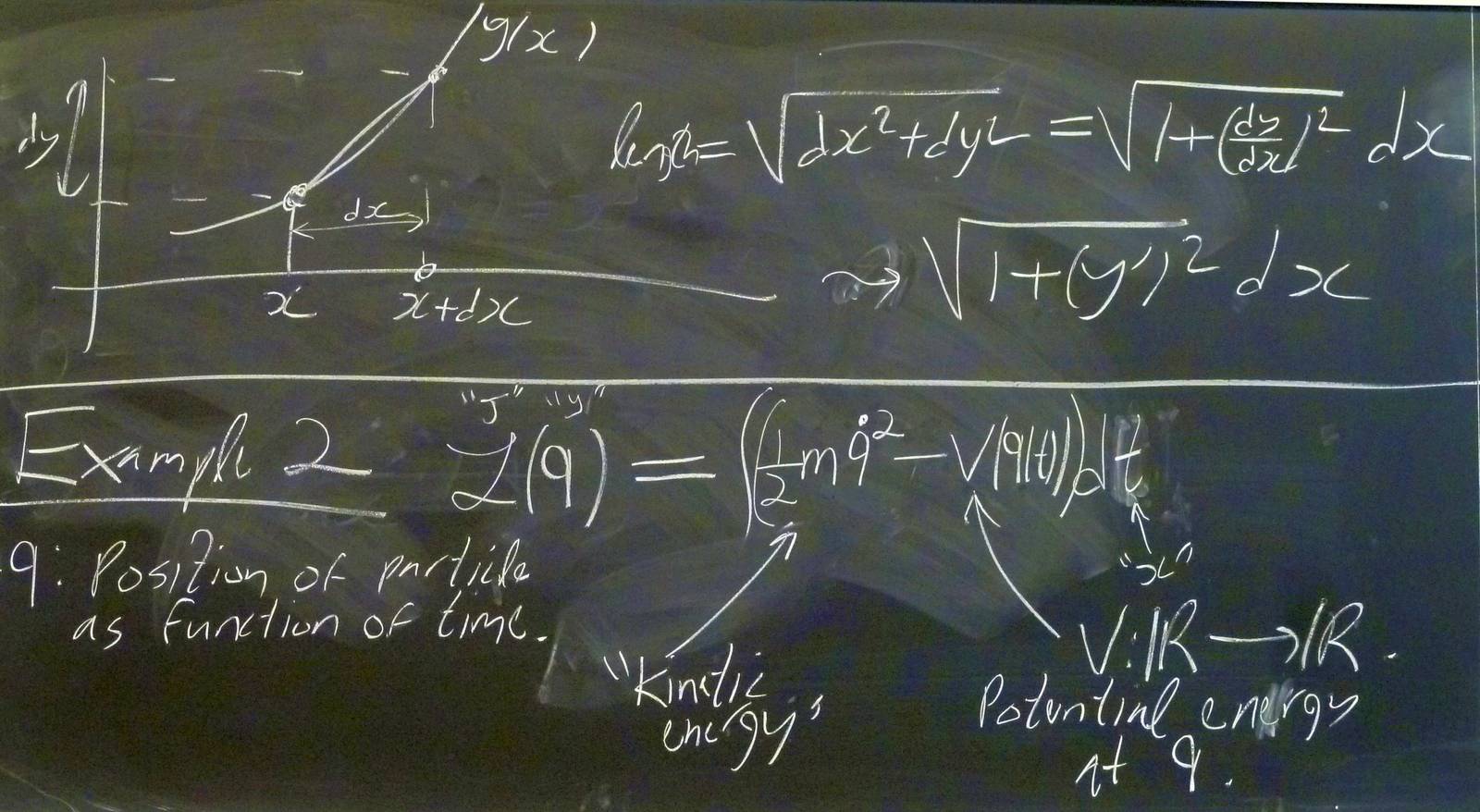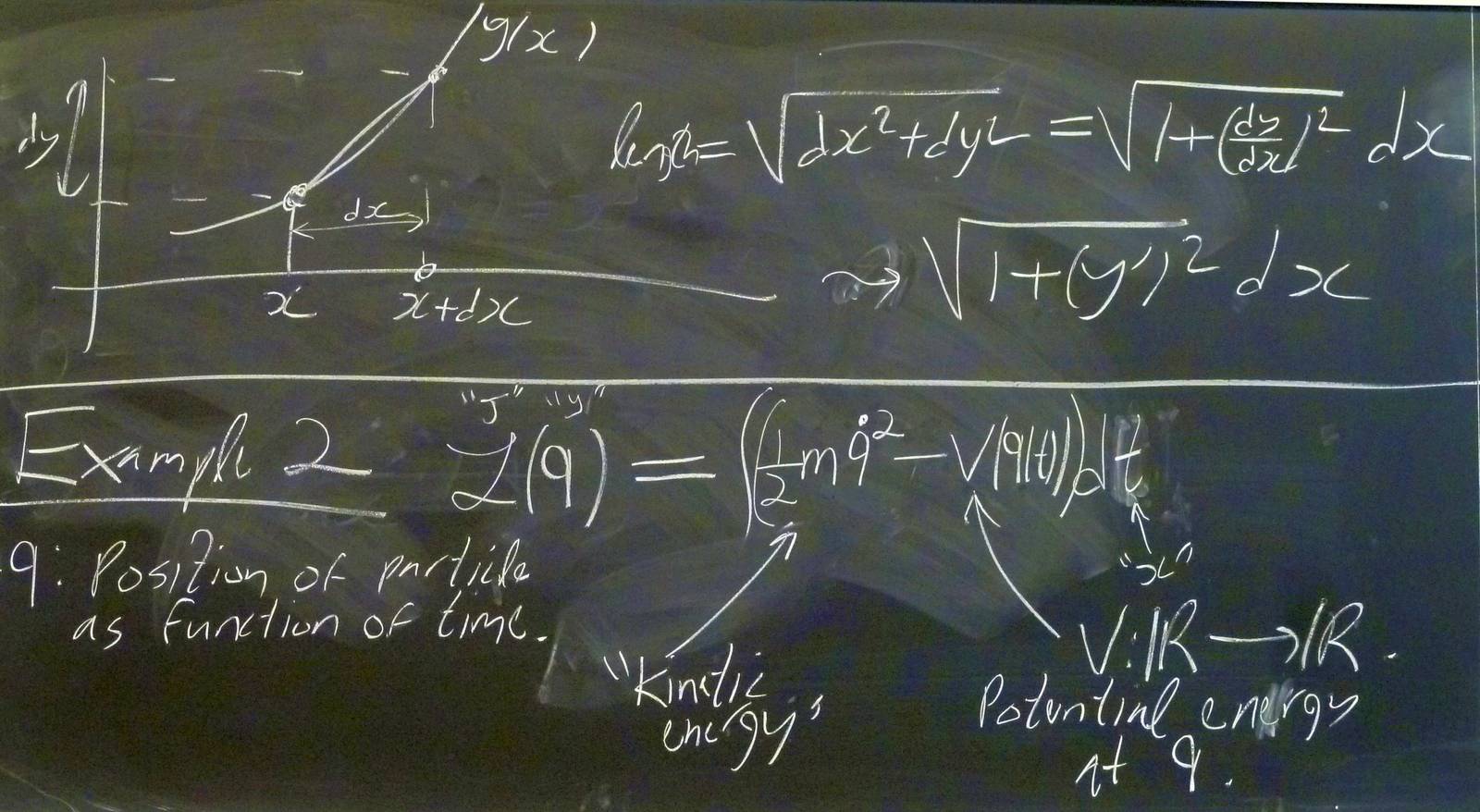
121002-094521: Example: Classical mechanics. @12_267 @Blackboard Shots @Academic Pensieve @Dror Bar-Natan

12_267-{	hide text
121204-100949:	The amplitudes when $q\to L$ (3).
121204-100307:	The amplitudes when $q\to L$ (2).
121204-095516:	The amplitudes when $q\to L$.
121204-095148:	Bounding amplitudes on the other side.
121204-094026:	The basic amplitudes theorem (2).
121204-093507:	The basic amplitudes theorem.
121204-093124:	Chaninging the independent variable (2).
121204-092337:	Chaninging the independent variable.
121204-092329:	Notes.
121203-100051:	Changing the independent variable (2).
121203-095636:	Changing the independent variable.
121203-094744:	The Sturm comparison theorem - comparing with Euler (3).
121203-094157:	The Sturm comparison theorem - comparing with Euler (2).
121203-093704:	The Sturm comparison theorem - comparing with Euler.
121203-093037:	The Sturm comparison theorem - studying Bessel.
121203-092424:	The Sturm comparison theorem - self comparisons (2).
121203-091617:	The Sturm comparison theorem - self comparisons.
121203-091524:	Notes and riddle.
121130-100324:	More on $y''+x^\alpha y=0$.
121130-095719:	The Sturm Comparison Theorem (3).
121130-095336:	The Sturm Comparison Theorem (2).
121130-095035:	The Sturm Comparison Theorem.
121130-094519:	$y''+x^\alpha y=0$.
121130-094107:	The non-oscillation theorem (5).
121130-093715:	The non-oscillation theorem (4).
121130-093107:	The non-oscillation theorem (3).
121130-092351:	The non-oscillation theorem (2).
121130-091916:	The non-oscillation theorem.
121130-091418:	Reminders
121130-091002:	Today's Catalan.
121127-100434:	Changing the dependent variable (3).
121127-095841:	Changing the dependent variable (2).
121127-095243:	Changing the dependent variable.
121127-094605:	The basic oscillation theorem (3).
121127-094055:	The basic oscillation theorem (2).
121127-093543:	The basic oscillation theorem.
121127-093006:	Restoring forces, the case of $q<0$.
121127-091026:	Airy's equation - why?
121127-091017:	Announcements.
121126-100200:	The hardest case - $\alpha_1-\alpha_2\in{\mathbb N}_{>0}$.
121126-095126:	The case of a double root (2).
121126-094748:	The case of a double root.
121126-094123:	Faking the graph of $x^{1/2}\cos(\frac12\log x)$.
121126-093828:	The easy case with complex numbers.
121126-093307:	The easy case.
121126-092606:	The fundamental series of $J_{1/3}$.
121126-091701:	Reminders, the fundamental series.
121123-100409:	RSP at order 2 (5).
121123-100024:	RSP at order 2 (4).
121123-095637:	RSP at order 2 (3).
121123-095031:	RSP at order 2 (2).
121123-094756:	RSP at order 2.
121123-094145:	RSP at order 1 (4).
121123-093629:	RSP at order 1 (3).
121123-093057:	RSP at order 1 (2).
121123-092500:	RSP at order 1.
121123-091716:	Today's topics.
121123-091132:	Riddle along.
121120-100237:	Proof of Fuchs' theorem (3).
121120-095532:	Proof of Fuchs' theorem (2).
121120-094617:	Proof of Fuchs' theorem.
121120-093509:	Fuchs' theorem.
121120-092913:	The Airy equation by power series (4).
121120-091425:	The Airy equation by power series (3).
121119-100238:	The Airy equation by power series (2).
121119-095656:	The Airy equation by power series.
121119-095030:	Examples for functions given by a formula (2).
121119-094324:	Examples for functions given by a formula.
121119-093656:	On functions given by a formula.
121119-093305:	The radius of convergence of a series (2).
121119-092529:	The radius of convergence of a series.
121119-092128:	$\pi$ is irrational.
121119-091004:	A proposition by Samer Seraj.
121116-100323:	A bit about convergence of series (2).
121116-095425:	A bit about convergence of series.
121116-094936:	Solving using power series (2).
121116-094011:	Solving using power series.
121116-092615:	Power series - motivation.
121116-091938:	Wronskians and $\cos^2 x + \sin^2 x$.
121116-091126:	Riddle Along.
121109-100032:	The case of 2nd order linear ODEs.
121109-095425:	Differetiating the Wronskian.
121109-094907:	Differetiating derivatives (3).
121109-094707:	Differetiating derivatives (2).
121109-094123:	Differetiating derivatives.
121109-093513:	The Wronskian.
121109-093219:	Global existence for linear systems (2).
121109-092640:	Global existence for linear systems.
121109-091529:	Claims and Debts of systems of ODEs.
121106-215845:	Challenges.
121106-215829:	A differential equation for the generating function of the $A_n$ (2).
121106-215243:	A differential equation for the generating function of the $A_n$.
121106-215031:	A recursion for $A_n$.
121106-214712:	The generating function of $C_n$ (2).
121106-214107:	The generating function of $C_n$.
121106-213547:	A recursive formula for the Catalan numbers $C_n$.
121106-212459:	$A_n$ and $C_n$.
121106-212016:	Debts on systems.
121106-210901:	Riddles Along.
121105-110135:	Proof of the invertibility claim (2).
121105-105750:	Proof of the invertibility claim.
121105-105456:	The non-homogeneous case using a Fundamental Matrix (4).
121105-105104:	The non-homogeneous case using a Fundamental Matrix (3).
121105-104645:	The non-homogeneous case using a Fundamental Matrix (2).
121105-104144:	The non-homogeneous case using a Fundamental Matrix.
121105-103615:	The non-homogeneous case by diagonalization (5).
121105-103301:	The non-homogeneous case by diagonalization (4).
121105-102738:	The non-homogeneous case by diagonalization (3).
121105-102024:	The non-homogeneous case by diagonalization (2).
121105-101538:	The non-homogeneous case by diagonalization.
121105-101031:	Read ahead, riddle along.
121030-095809:	Example with a repeated eigenvalue (2).
121030-095415:	Example with a repeated eigenvalue.
121030-095102:	Exponentiating a Jordan block.
121030-094321:	The Jordan form theorem (2).
121030-093500:	The Jordan form theorem.
121030-093236:	Example with distinct eigenvalues (3).
121030-092306:	Example with distinct eigenvalues (2).
121030-091915:	Example with distinct eigenvalues.
121030-091559:	Reminders.
121030-091036:	Announcements.
121029-100048:	Properties of matrix exponentiation (6).
121029-095744:	Properties of matrix exponentiation (5).
121029-095326:	Properties of matrix exponentiation (4).
121029-094547:	Properties of matrix exponentiation (3).
121029-094025:	Properties of matrix exponentiation (2).
121029-093558:	Properties of matrix exponentiation.
121029-092858:	Convergence.
121029-091928:	Exponentiation via the Taylor series.
121029-091107:	Announcements.
121023-100040:	Matrix exponentiation (2).
121023-095938:	Matrix exponentiation.
121023-095149:	A baby version.
121023-094809:	Systems of linear equations.
121023-093831:	Undetermined coefficients (4).
121023-092351:	Undetermined coefficients (3).
121023-091741:	Undetermined coefficients (2).
121023-091718:	Pre-exam office hours.
121022-100052:	Undetermined coefficients.
121022-095206:	Reduction of order.
121022-094433:	Multiple roots (5).
121022-093955:	Multiple roots (4).
121022-093804:	Multiple roots (3).
121022-093504:	An aside on the Leibniz rule for higher derivatives.
121022-092921:	Multiple roots (2).
121022-092104:	Multiple roots.
121022-091332:	The case of distinct roots.
121022-090631:	TT, Read Along, Riddle Along.
121019-095816:	From complex back to real.
121019-095806:	Distinct real roots, complex root.
121019-094930:	Differential operator language.
121019-094408:	The guessing method.
121019-094033:	Constant coefficients homogeneous high order ODEs (2).
121019-094024:	Constant coefficients homogeneous high order ODEs.
121019-093128:	Numerical Integration (3).
121019-093058:	Numerical Integration (2).
121019-091840:	Numerical Integration.
121016-093936:	Runge-Kutta.
121016-093634:	A general scheme.
121016-093057:	Local analysis of improved Euler (2).
121016-092401:	Local analysis of improved Euler.
121016-091448:	Euler and improved Euler.
121016-090737:	Term test info and riddle.
121012-095603:	Numerical methods, starting from the silly (3).
121012-095555:	Numerical methods, starting from the silly (2).
121012-094800:	Numerical methods, starting from the silly.
121012-094127:	E-L is a gradient!
121012-093338:	Lagrange multipliers in CoV.
121012-092651:	The Lagrange Multipliers Theorem (3).
121012-092050:	The Lagrange Multipliers Theorem (2).
121012-091426:	The Lagrange Multipliers Theorem.
121012-090625:	Read along and riddle along.
121009-095640:	Directional derivatives.
121009-095113:	The isoperimetric inequality (4).
121009-094819:	The isoperimetric inequality (3).
121009-094131:	The isoperimetric inequality (2).
121009-093631:	Lagrange multipliers in ${\mathbb R}^2$ (4).
121009-093049:	Lagrange multipliers in ${\mathbb R}^2$ (3).
121009-092523:	Lagrange multipliers in ${\mathbb R}^2$ (2).
121009-092511:	Lagrange multipliers in ${\mathbb R}^2$.
121009-091240:	The isoperimetric inequality.
121005-095531:	Bread with least crust.
121005-094811:	The brachistochrone, again.
121005-094413:	Conservation of energy (2).
121005-094106:	Conservation of energy.
121005-092726:	Conservation of momentum.
121005-092109:	Reminder of Euler-Lagrange.
121005-090823:	Notes and riddles.
121002-103950:	Properly writing Euler-Lagrange and the brachistochrone.
121002-103247:	$F=ma$ (2).
121002-102822:	Deriving Euler-Lagrange (5), $F=ma$.
121002-102506:	Deriving Euler-Lagrange (4).
121002-101904:	Deriving Euler-Lagrange (3).
121002-101423:	Deriving Euler-Lagrange (2).
121002-095520:	Deriving Euler-Lagrange.
121002-095243:	Example: The brachistochrone.
121002-094521:	Example: Classical mechanics.
121002-094030:	Example: Power lines.
121002-092726:	The basic calculus of variations problem.
121002-092032:	Back to the chain rule (2).
121002-091704:	Back to the chain rule.
121002-090739:	Today's riddle.
121001-095749:	Calculus of variations (2).
121001-095740:	Higher order equations, calculus of variations.
121001-094905:	The fundamental theorem: higher order equations.
121001-094116:	The fundamental theorem: systems (2).
121001-093509:	The fundamental theorem: systems.
121001-093010:	The fundamental theorem: uniqueness (2).
121001-092946:	The fundamental theorem: uniqueness.
121001-091541:	Review of the fundamental theorem.
121001-090909:	Computing $(x^x)'$.
120928-095846:	The Fundamental Theorem: Uniform Convergence.
120928-094804:	The Fundamental Theorem: $\phi_n-\phi_{n-1}$ is well-bounded (2).
120928-094102:	The Fundamental Theorem: $\phi_n-\phi_{n-1}$ is well-bounded.
120928-093027:	The Fundamental Theorem: $\phi_n$ is well-defined.
120928-092238:	The Fundamental Theorem: the $y'=y$ example.
120928-091714:	The Fundamental Theorem: Statement.
120925-095319:	The Fundamental Theorem (3).
120925-094906:	The Fundamental Theorem (2).
120925-094303:	The Fundamental Theorem.
120925-093754:	The Lipschitz Condition.
120925-092443:	Wishful thinking (3).
120925-092029:	Wishful thinking (2).
120925-091230:	Wishful thinking.
120925-090721:	Riddle Along.
120924-095914:	Integrating factors (3).
120924-095800:	Integrating factors (2).
120924-095319:	Integrating factors.
120924-095019:	Exact equations (5).
120924-094422:	Exact equations (4).
120924-093936:	Exact equations (3).
120924-093412:	Exact equations (2).
120924-092906:	Exact equations.
120924-092111:	Partial derivatives commute (2).
120924-091545:	Partial derivatives commute.
120924-090840:	Show and tell (2).
120924-090831:	Show and tell.
120921-095745:	Notes for September 21 (6).
120921-095252:	Notes for September 21 (5).
120921-095245:	Notes for September 21 (4).
120921-093121:	Notes for September 21 (3).
120921-092710:	Notes for September 21 (2).
120921-092353:	Notes for September 21.
120918-095852:	Homogeneous Equations (2).
120918-095416:	Homogeneous Equations.
120918-094717:	Autonomous Equations (2).
120918-094527:	Autonomous Equations.
120918-093915:	Changing source and target coordinates (2).
120918-093421:	Changing source and target coordinates.
120918-091850:	Escape Velocities (2).
120918-091728:	Escape Velocities.
120918-090713:	Riddle Along.
120917-095813:	Escape velocities (2).
120917-095323:	Escape velocities.
120917-094437:	Separable equations: the easy to justify way (2).
120917-093948:	Separable equations: the easy to justify way.
120917-093027:	Separable equations: the easy to remember way.
120917-091853:	The general problem, separable equations.
120917-090926:	Comments and riddles.
120914-095607:	First order linear, non-homgeneous (5).
120914-095435:	First order linear, non-homgeneous (4).
120914-095224:	First order linear, non-homgeneous (3).
120914-094700:	First order linear, non-homgeneous (2).
120914-093953:	First order linear, non-homgeneous.
120914-093309:	First order linear homogeneous (2).
120914-092628:	First order linear homogeneous.
120914-091936:	$y'=f$ and first order linear homogeneous.
120914-090342:	Read along and riddle along.
120911-094639:	This is a cycloid (2).
120911-093941:	This is a cycloid.
120911-093629:	Solving the equation (2).
120911-093043:	Solving the equation.
120911-092453:	Brachistochrone review.
120910-100221:	Deriving the brachistochrone equation (2).
120910-095542:	Deriving the brachistochrone equation.
120910-094435:	Fermat's principle and Snell's law.
120910-093559:	The Brachistochrone problem.
120910-092814:	A messy example.
120910-092025:	What's a differential equation?
}